
【题目】已知:抛物线y=x2+(b﹣1)x﹣5.
(1)写出抛物线的开口方向和它与y轴交点的坐标;
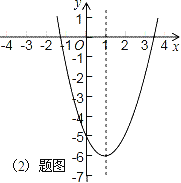
(2)若抛物线的对称轴为直线x=1,求b的值,并画出抛物线的草图(不必列表);
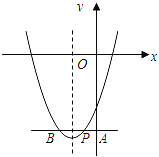
(3)如图,若b>3,过抛物线上一点P(﹣1,c)作直线PA⊥y轴,垂足为A,交抛物线于另一点B,且BP=2PA,求这条抛物线所对应的二次函数解析式.
【答案】(1)、开口向上;(0,﹣5);(2)、b=1;图形见解析;(3)、y=x2+4x﹣5
【解析】
试题分析:(1)、根据a值大于0,判断抛物线的开口向上,令x=0求出函数值y,就是抛物线与y轴的交点坐标;(2)、根据对称轴解析式列式求出b的值,从而得到抛物线解析式,再根据抛物线与坐标轴的交点与顶点坐标作出草图即可;(3)、先根据b>3判断出点P在对称轴的左侧,然后根据BP=2PA求出点B的坐标,然后把点P、B的坐标代入抛物线解析式,利用待定系数法求出b、c的值,即可写出该抛物线对应的二次函数解析式.[或者根据点BP的中点在抛物线的对称轴上,利用对称轴解析式列式进行计算求解b的值.
试题解析:(1)、∵a=1>0, ∴抛物线开口向上, 当x=0时,y=02+(b﹣1)×0﹣5=﹣5,
∴它与y轴的交点坐标为(0,﹣5);
(2)、抛物线的对称轴为x=1, ∴﹣![]() =﹣
=﹣![]() =1, 解得b=﹣1,故抛物线的解析式为y=x2﹣2x﹣5;
=1, 解得b=﹣1,故抛物线的解析式为y=x2﹣2x﹣5;
图象如右;
(3)、∵b>3, ∴抛物线的对称轴x=﹣![]() =﹣
=﹣![]() <﹣1, ∴对称轴在点P的左侧,
<﹣1, ∴对称轴在点P的左侧,
∵直线PA⊥y轴,且P(﹣1,c),BP=2PA, ∴点B的坐标为(﹣3,c),
把点B(﹣3,c)、P(﹣1,c)代入抛物线解析式y=x2+(b﹣1)x﹣5得b=5,c=-8
∴抛物线所对应的二次函数解析式为y=x2+4x﹣5;


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上.将△ABC绕点A顺时针旋转90°得到△AB1C1.
(1)在网格中画出△AB1C1;
(2)计算点B旋转到B1的过程中所经过的路径长.(结果保留π)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形ABCD中,动点P从A点出发,以每秒1个单位长度的速度沿AB向B点运动,同时动点Q从B点出发,以每秒2个单位长度的速度沿BC→CD方向运动,当P运动到B点时,P、Q两点同时停止运动.设P点运动的时间为t秒,△APQ的面积为S,则表示S与t之间的函数关系的图象大致是( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2010年5月1日至2010年10月31日期间在上海举行的世界博览会总投资约450亿元人民币,其中“450亿”用科学记数法表示为( )元.
A.4.5×1010
B.4.5×109
C.4.5×108
D.0.45×109
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过A(﹣4,0)、B(1,0)、C(0,3)三点,直线y=mx+n经过A(﹣4,0)、C(0,3)两点.
(1)写出方程ax2+bx+c=0的解;
(2)若ax2+bx+c>mx+n,写出x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
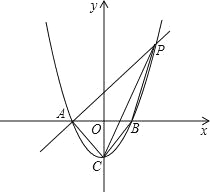
【题目】已知如图:抛物线y=x2﹣1与x轴交于A、B两点,与y轴交于点C.
(1)求A、B、C三点的坐标.
(2)过点A作AP∥CB交抛物线于点P,求四边形ACBP的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com