
【题目】已知菱形ABCD的对角线相交于O,点E,F分别在边AB、BC上,且BE=BF,射线EO,FO分别交边CD、AD于G,H.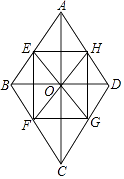
(1)求证:四边形EFGH为矩形;
(2)若OA=4,OB=3,求EG的最小值.
【答案】
(1)证明:∵四边形ABCD是菱形,
∴OA=OC,OB=OD,AB∥CD,AD∥BC,
∴∠BAO=∠DCO,∠AOE=∠GOC,
∴△AOE≌△COG(ASA),
∴OE=OG,
同理得:OH=OF,
∴四边形EFGH是平行四边形,
∵BE=BF,∠ABD=∠CBD,OB=OB,
∴△EBO≌△FBO,
∴OE=OF,
∴EG=FH,
∴四边形EFGH是矩形;
(2)解:∵垂线段最短,
∴当OE⊥AB时,OE最小,
∵OA=4,OB=3,∠AOB=90°,
∴AB2=OA2+OB2=25,
∴AB=5,
∴ ![]() OA×OB=
OA×OB= ![]() AB×OE,
AB×OE,
3×4=5×OE,
OE= ![]() ,
,
∵OE=OG,
∴EG= ![]() .
.
答:EG的最小值是 ![]() .
.
【解析】(1)利用菱形的性质可证得四边形EFGH的对角线互相平分,证出它是平行四边形,再证出其对角线相等,得出它是矩形;(2)求EG的最小值也就是OE 的最小值,根据垂线段最短,可知当OEOE⊥AB时,OE最小,进而EGz最小.
【考点精析】解答此题的关键在于理解菱形的性质的相关知识,掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.


科目:初中数学 来源: 题型:
【题目】下图示为若干名学生每分钟脉搏跳动次数的频数分布折线.
(1)求学生的总人数;
(2)分布在两端虚设的两组的组中值分别是多少?
(3)估计样本的中位数.
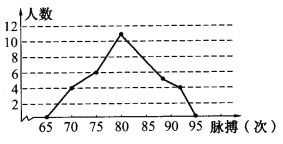
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,长方形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2, 0)同时出发,沿长方形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位长度秒匀速运动,物体乙按顺时针方向以2个单位长度秒匀速运动,则两个物体运动后的第2020次相遇点的坐标是( )

A.(2,0)B.(-1,-1)C.( -2,1)D.(-1, 1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交弧AB于点E,以点O为圆心,OC的长为半径作弧CD交OB于点D,若OA=4,则阴影部分的面积为 . 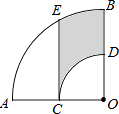
查看答案和解析>>
科目:初中数学 来源: 题型:
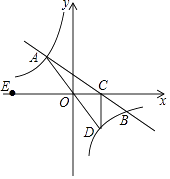
【题目】如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y= ![]() (m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(12,n)
(m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(12,n)
, OA=10,E为x轴负半轴上一点,且tan∠AOE= ![]() .
.
(1)求该反比例函数和一次函数的解析式;
(2)延长AO交双曲线于点D,连接CD,求△ACD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学在甲乙两家超市发现他看中的一套运动服的单价相同,书包单价也相同.运动服和书包单价之和是452元,且运动服的单价比书包单价的4倍少8元.
(1)求该同学看中的运动服和书包的单价各是多少元?
(2)某一天该同学上街,恰好赶上商家促销,甲超市所有商品打八折销售,乙超市全场每购满100元返购物券30元销售(不足100元不返券,购物券全场通用),但他只带了400元钱,如果他只在一家超市购买看中的这两样物品,请说明他能在哪一家购买?若两家都可以选择,在哪一家购买更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为保持水土,美化环境,W中学准备在从校门口到柏油公路的这一段土路的两侧栽一些树,并要求土路两侧树的棵数相等间距也相等,且首、尾两端均栽上树,现在学校已备好一批树苗,若间隔30米栽一棵,则缺少22棵;若间隔35米栽一棵,则缺少14棵
(1)求学校备好的树苗棵数.
(2)某苗圃负责人听说W中学想在校外土路两旁栽树的上述情况后,觉得两树间距太大,既不美观,又影响防风固沙的效果,决定无偿支援W中学300棵树苗.请问,这些树苗加上学校自己备好的树苗,间隔5米栽一棵,是否够用?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com