
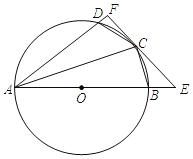
【题目】如图,四边形![]() 内接于⊙
内接于⊙![]() ,点
,点![]() 在
在![]() 上,
上,![]() ,过点
,过点![]() 作⊙
作⊙![]() 的切线,分别交
的切线,分别交![]() ,
,![]() 的延长线于点
的延长线于点![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)AD![]() ,详情见解析;
,详情见解析;
【解析】
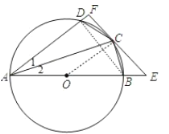
(1)连接OC,如图,先证明OC∥AF,再根据切线的性质得OC⊥EF,从而得到AF⊥EF;
(2)先利用OC∥AF得到∠COE=∠DAB,在Rt△OCE中,设OC=r,利用余弦的定义得到![]() ,解得r=4,连接BD,如图,根据圆周角定理得到∠ADB=90°,然后根据余弦的定义可计算出AD的长.
,解得r=4,连接BD,如图,根据圆周角定理得到∠ADB=90°,然后根据余弦的定义可计算出AD的长.
(1)证明:连接OC,
∵CD=BD,
∴弧CD=弧BC,
∴∠1=∠2,
∵OA=OC,
∴∠2=∠OCA,
∴∠1=∠OCA,
∴OC∥AF,
∵EF为切线,
∴OC⊥EF,
∴AF⊥EF;
(2)∵OC∥AF,
∴∠COE=∠DAB,
在Rt△OCE中,设OC=r,
∵cos∠COE=cos∠DAB=![]() ,
,
即![]() ,
,
解得r=4,
连接BD,如图,
∵AB为直径,
∴∠ADB=90°,
在Rt△ADB中,cos∠DAB=![]() ,
,
∴AD![]() ;
;


科目:初中数学 来源: 题型:
【题目】阅读下面材料:在数学课上,老师提出如下问题:
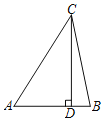
已知:如图,CD是△ABC的高,
尺规作图:在线段CD上求作点P,使∠APB=45°(保留作图痕迹,写出作法),
请回答:你推出∠APB=45°的依据是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在小正方形组成网格图中,四边形 ABCD 的顶点都在格点上,如图所示.则下列结论错 误的是( )
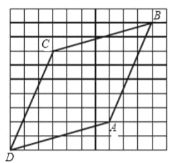
A.![]() B.
B.![]()
C.四边形![]() 是菱形D.将边
是菱形D.将边![]() 向右平移
向右平移![]() 格,再向上平移
格,再向上平移![]() 格就与边
格就与边![]() 重合
重合
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,长、宽均为3,高为8的长方体容器,放置在水平桌面上,里面盛有水,水面高为6,绕底面一棱长进行旋转倾斜后,水面恰好触到容器口边缘,图2是此时的示意图,则图2中水面高度为( )
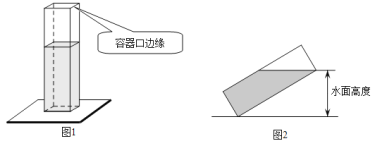
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系![]() 中的点
中的点![]() 和
和![]() (半径为
(半径为![]() ),给出如下定义:若点
),给出如下定义:若点![]() 关于点
关于点![]() 的对称点为
的对称点为![]() ,且
,且![]() ,则称点
,则称点![]() 为
为![]() 的称心点.
的称心点.
(1)当![]() 的半径为2时,
的半径为2时,
①如图1,在点![]() ,
,![]() ,
,![]() 中,
中,![]() 的称心点是 ;
的称心点是 ;
②如图2,点![]() 在直线
在直线![]() 上,若点
上,若点![]() 是
是![]() 的称心点,求点
的称心点,求点![]() 的横坐标
的横坐标![]() 的取值范围;
的取值范围;
(2)![]() 的圆心为
的圆心为![]() ,半径为2,直线
,半径为2,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,
,![]() .若线段
.若线段![]() 上的所有点都是
上的所有点都是![]() 的称心点,直接写出
的称心点,直接写出![]() 的取值范围.
的取值范围.
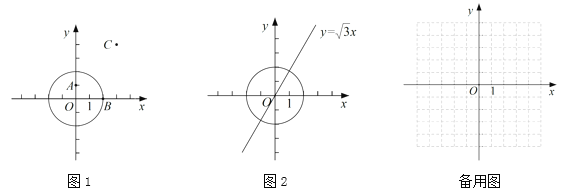
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=![]() (n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(1)求一次函数与反比例函数的解析式;
(2)记两函数图象的另一个交点为E,求△CDE的面积;
(3)直接写出不等式kx+b≤![]() 的解集.
的解集.
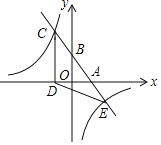
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现今“微信运动”被越来越多的人关注和喜爱,某数学兴趣小组随机调查了我市![]() 名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
步数 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

请根据以上信息,解答下列问题:
(1)写出![]() ,
,![]() ,
,![]() ,
,![]() 的值并补全频数分布直方图;
的值并补全频数分布直方图;
(2)我市约有![]() 名教师,用调查的样本数据估计日行走步数超过
名教师,用调查的样本数据估计日行走步数超过![]() 步(包含
步(包含![]() 步)的教师有多少名?
步)的教师有多少名?
(3)若在![]() 名被调查的教师中,选取日行走步数超过
名被调查的教师中,选取日行走步数超过![]() 步(包含
步(包含![]() 步)的两名教师与大家分享心得,用树形图或列表法求被选取的两名教师恰好都在
步)的两名教师与大家分享心得,用树形图或列表法求被选取的两名教师恰好都在![]() 步(包含
步(包含![]() 步)以上的概率.
步)以上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆共有80间客房.宾馆负责人根据经验作出预测:今年7月份,每天的房间空闲数y(间)与定价x(元/间)之间满足y=![]() x﹣42(x≥168).若宾馆每天的日常运营成本为5000元,有客人入住的房间,宾馆每天每间另外还需支出28元的各种费用,宾馆想要获得最大利润,同时也想让客人得到实惠,应将房间定价确定为( )
x﹣42(x≥168).若宾馆每天的日常运营成本为5000元,有客人入住的房间,宾馆每天每间另外还需支出28元的各种费用,宾馆想要获得最大利润,同时也想让客人得到实惠,应将房间定价确定为( )
A.252元/间B.256元/间C.258元/间D.260元/间
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com