
【题目】阅读下面材料:在数学课上,老师提出如下问题:
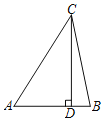
已知:如图,CD是△ABC的高,
尺规作图:在线段CD上求作点P,使∠APB=45°(保留作图痕迹,写出作法),
请回答:你推出∠APB=45°的依据是 .
【答案】作图及作法见解析;一条弧所对的圆周角等于它所对圆心角的一半
【解析】
先作出AB的垂直平分线GH交AB于E,然后在GH上截取EF=AE,则有∠AFB=90°,再以F为圆心,AF的长为半径画圆交CD于一点即为点P,根据圆周角定理可得出∠APB=![]() ∠AFB=45°.
∠AFB=45°.
解:如图,
(1)分别以点A和点B为圆心,大于![]() AB的长为半径作弧,两弧相交于G、H两点;
AB的长为半径作弧,两弧相交于G、H两点;
(2)作直线GH交AB于点E;
(3)在直线GH截取EF=AE;
(4)以点F为圆心,AF的长为半径画圆交CD于点P.
则点P即为所求.
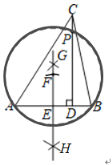
由作法可知GH垂直平分AB,AE=EF=BE,得到∠AFB=90°,
∴根据圆周角定理得到∠APB=![]() ∠AFB=45°.
∠AFB=45°.
故答案为:一条弧所对的圆周角等于它所对圆心角的一半.


科目:初中数学 来源: 题型:
【题目】我们将![]() 、
、![]() 称为一对“对偶式”,因为
称为一对“对偶式”,因为![]()
![]() ,所以构造“对偶式”再将其相乘可以有效的将
,所以构造“对偶式”再将其相乘可以有效的将![]() 和
和![]() 中的“
中的“![]() ”去掉.于是二次根式除法可以这样解:如
”去掉.于是二次根式除法可以这样解:如![]() ,
,![]()
![]() .像这样,通过分子,分母同乘以一个式子把分母中的根号化去或把根号中的分母化去,叫做分母有理化.根据以上材料,理解并运用材料提供的方法,解答以下问题:
.像这样,通过分子,分母同乘以一个式子把分母中的根号化去或把根号中的分母化去,叫做分母有理化.根据以上材料,理解并运用材料提供的方法,解答以下问题:
(1)比较大小![]() ________
________![]() (用“
(用“![]() ”、“
”、“![]() ”或“
”或“![]() ”填空);
”填空);
(2)已知![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)计算:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,点B位于(4,0)、(5,0)之间,与y轴交于点C,对称轴为直线x=2,直线y=﹣x+c与抛物线y=ax2+bx+c交于C,D两点,D点在x轴上方且横坐标小于5,则下列结论:①4a+b+c>0;②a﹣b+c<0;③m(am+b)<4a+2b(其中m为任意实数);④a<﹣1,其中正确的是( )

A.①②③④B.①②③C.①②④D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展“我最喜爱的一项体育活动”调查,要求每名学生必选且只能选一项.现随机抽查了部分学生,并将其结果绘制成如下不完整的条形图和扇形图.
抽取的学生最喜欢体育活动的条形统计图
抽取的学生最喜欢体育活动的扇形统计图
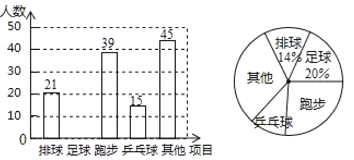
请结合以上信息解答下列问题:
(1)在这次调查中一共抽查了_____学生,扇形统计图中“乒乓球”所对应的圆心角为_____度,并请补全条形统计图;
(2)己知该校共有1200名学生,请你估计该校最喜爱跑步的学生人数;
(3)若在“排球、足球、跑步、乒乓球”四个活动项目任选两项设立课外兴趣小组,请用列表法或画树状图的方法求恰好选中“排球、乒乓球”这两项活动的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
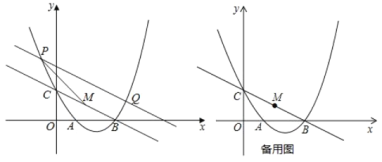
【题目】抛物线![]() 与x轴交于A、B两点,与y轴交于C,其中B(4,0),C(0,2),点P为抛物线上一动点,过点P作PQ平行BC交抛物线于Q.
与x轴交于A、B两点,与y轴交于C,其中B(4,0),C(0,2),点P为抛物线上一动点,过点P作PQ平行BC交抛物线于Q.
(1)求抛物线的解析式;
(2)①当P、Q两点重合时,PQ所在直线解析式为 ;②在①的条件下,取线段BC中点M,连接PM,判断以点P、O、M、B为顶点的四边形是什么四边形,并说明理由?
(3)已知N(0,![]() ),连接BN,K(3,0),KE∥y轴,交BN于E,x轴上有一动点F,∠EFN=60°,求OF的长.
),连接BN,K(3,0),KE∥y轴,交BN于E,x轴上有一动点F,∠EFN=60°,求OF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
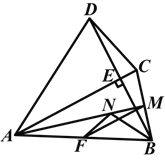
【题目】(2014山东淄博)如图,四边形ABCD中,AC⊥BD交BD于点E,点F,M分别是AB,BC的中点,BN平分∠ABE交AM于点N,AB=AC=BD,连接MF,NF.
(1)判断△BMN的形状,并证明你的结论;
(2)判断△MFN与△BDC之间的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是直径AB上的一点,AB=6,CP⊥AB交半圆![]() 于点C,以BC为直角边构造等腰Rt△BCD,∠BCD=90°,连接OD.
于点C,以BC为直角边构造等腰Rt△BCD,∠BCD=90°,连接OD.

小明根据学习函数的经验,对线段AP,BC,OD的长度之间的关系进行了探究.
下面是小明的探究过程,请补充完整:
(1)对于点P在AB上的不同位置,画图、测量,得到了线段AP,BC,OD的长度的几组值,如下表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置… | |
AP | 0.00 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | … |
BC | 6.00 | 5.48 | 4.90 | 4.24 | 3.46 | 2.45 | … |
OD | 6.71 | 7.24 | 7.07 | 6.71 | 6.16 | 5.33 | … |
在AP,BC,OD的长度这三个量中,确定________的长度是自变量,________的长度和________的长度都是这个自变量的函数;
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数的图象;

(3)结合函数图象,解决问题:当OD=2BC时,线段AP的长度约为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com