Question

1．顺次连结四边形四条边的中点，所得的四边形是矩形，则原四边形一定是（　　）

• A． 平行四边形
• B． 对角线互相垂直的四边形
• C． 菱形
• D． 对角线相等的四边形

Answer 1

分析 这个四边形ABCD的对角线AC和BD的关系是互相垂直．理由为：根据题意画出相应的图形，如图所示，由四边形EFGH为矩形，根据矩形的四个角为直角得到∠FEH=90°，又EF为三角形ABD的中位线，根据中位线定理得到EF与DB平行，根据两直线平行，同旁内角互补得到∠EMO=90°，同理根据三角形中位线定理得到EH与AC平行，再根据两直线平行，同旁内角互补得到∠AOD=90°，根据垂直定义得到AC与BD垂直．

解答 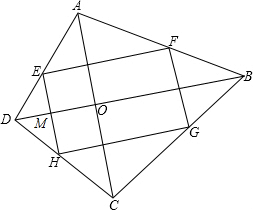解：∵四边形EFGH是矩形，
∴∠FEH=90°，
又∵点E、F、分别是AD、AB、各边的中点，
∴EF是三角形ABD的中位线，
∴EF∥BD，
∴∠FEH=∠OMH=90°，
又∵点E、H分别是AD、CD各边的中点，
∴EH是三角形ACD的中位线，
∴EH∥AC，
∴∠OMH=∠COB=90°，
即AC⊥BD，
故原图形一定是：对角线垂直的四边形．
故选：B．

点评 此题考查了矩形的性质，三角形的中位线定理，以及平行线的性质．这类题的一般解法是：借助图形，充分抓住已知条件，找准问题的突破口，由浅入深多角度，多侧面探寻，联想符合题设的有关知识，合理组合发现的新结论，围绕所探结论环环相加，步步逼近，所探结论便会被“逼出来”．