【题目】已知等腰三角形一腰上的中线将它的周长分为9和12两部分，则腰长为_______，底边长为_______．
星级口算天天练系列答案科目：初中数学 来源： 题型：
【题目】如图，AB是⊙O直径，D为⊙O上一点，AT平分∠BAD交⊙O于点T，过T作AD的垂线交AD的延长线于点C．
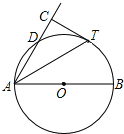
（1）求证：CT为⊙O的切线；
（2）若⊙O半径为2，CT=
，求AD的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】综合与实践
（1）（探索发现）在
中. 
，
，点
为直线
上一动点（点不与点
，
重合），过点作
交直线
于点
，将
绕点顺时针旋转
得到
，连接
．
如图（1），当点在线段上，且
时，试猜想：
①
与之间的数量关系：______；
②
______．
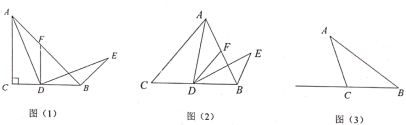
（2）（拓展探究）
如图（2），当点在线段上，且
时，判断与之间的数量关系及
的度数，请说明理由．
（3）（解决问题）
如图（3），在中，，
，，点在射线上，将绕点顺时针旋转得到，连接．当
时，直接写出的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数
（
，
为常数）.
（1）当
，
时，求二次函数的最小值；
（2）当
时，若在函数值
的情况下，只有一个自变量
的值与其对应，求此时二次函数的解析式；
（3）当
时，若在自变量的值满足≤≤
的情况下，与其对应的函数值
的最小值为21，求此时二次函数的解析式.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在边长为2的正方形ABCD中，P为AB的中点，Q为边CD上一动点，设DQ=t（0≤t≤2），线段PQ的垂直平分线分别交边AD、BC于点M、N，过Q作QE⊥AB于点E，过M作MF⊥BC于点F．
（1）当t≠1时，求证：△PEQ≌△NFM；
（2）顺次连接P、M、Q、N，设四边形PMQN的面积为S，求出S与自变量t之间的函数关系式，并求S的最小值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】“爱心”帐篷集团的总厂和分厂分别位于甲、乙两市，两厂原来每周生产帐篷共9千顶，现某地震灾区急需帐篷14千顶，该集团决定在一周内赶制出这批帐篷．为此，全体职工加班加点，总厂和分厂一周内制作的帐篷数分别达到了原来的1.6倍、1.5倍，恰好按时完成了这项任务．
（1）在赶制帐篷的一周内，总厂和分厂各生产帐篷多少千顶？
（2）现要将这些帐篷用卡车一次性运送到该地震灾区的
两地，由于两市通住
两地道路的路况不同，卡车的运载量也不同．已知运送帐篷每千顶所需的车辆数、两地所急需的帐篷数如下表：
|
| ||
每千顶帐篷 所需车辆数 | 甲市 | 4 | 7 |
乙市 | 3 | 5 | |
所急需帐篷数（单位：千顶） | 9 | 5 | |
请设计一种运送方案，使所需的车辆总数最少．说明理由，并求出最少车辆总数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，对于点
和点
，给出如下定义：
若
，则称点
为点
的限变点．
例如：点
的限变点的坐标为，点
的限变点的坐标是
．
（1）①
的限变点的坐标是____________．
②若点在函数
图象上，其限变点在函数
的图象上，则函数的函数值
随
的增大而增大时自变量的取值范围是____________．
（2）若点在函数
的图象上，其限变点的纵坐标
的取值范围是
，求
的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB=AC=4，将△ABC绕点A顺时针旋转30°，得到△ACD，延长AD交BC的延长线于点E，则DE的长为__________
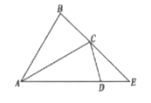
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，已知点
的坐标为
，点
分别是某函数图象与
轴、
轴的交点，点
是此图象上的一动点．设点的横坐标为，
的长为
，且与之间满足关系：
，则正确结论的序号是（ ）
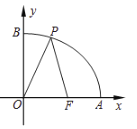
①
；②
；③当
时，
；④
的最大值是6．
A.①②③B.③④C.①②④D.①④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
