
【题目】在△ABC中,BA=BC,D,E是AC边上的两点,且满足∠DBE=![]() ∠ABC.
∠ABC.

(1)如图1,以点B为旋转中心,将△EBC按顺时针方向旋转,得到△E′BA(点C与点A重合,点E到点E′处),连接DE′.求证:DE′=DE;
(2)如图2,若∠ABC=90°,AD=4,EC=2,求DE的长.
【答案】(1)见解析;(2)2![]() .
.
【解析】
试题分析:(1)先根据旋转的性质得BE′=BE,∠E′BA=∠EBC,则∠E′BE=∠ABC,再利用∠DBE=![]() ∠ABC易得∠DBE′=∠DBE,根据“SAS”判断△BDE′≌△BDE,所以DE′=DE;
∠ABC易得∠DBE′=∠DBE,根据“SAS”判断△BDE′≌△BDE,所以DE′=DE;
(2)以点B为旋转中心,将△EBC按顺时针方向旋转90°得到△E′BA(点C与点A重合,点E到点E′处),如图2,利用等腰直角三角形的性质得∠BCE=∠BAD=45°,利用旋转的性质得∠BAE′=∠BCE=45°,AE′=CE=2,则∠DAE′=90°,在Rt△DAE′中利用勾股定理可计算出DE′=2![]() ,然后就根据(1)的结论即可得到DE=DE′=2
,然后就根据(1)的结论即可得到DE=DE′=2![]() .
.
(1)证明:∵以点B为旋转中心,将△EBC按顺时针方向旋转,得到△E′BA(点C与点A重合,点E到点E′处),
∴BE′=BE,∠E′BA=∠EBC,
∴∠E′BE=∠ABC,
∵∠DBE=![]() ∠ABC,
∠ABC,
∴∠DBE=![]() ∠E′BE,即∠DBE′=∠DBE,
∠E′BE,即∠DBE′=∠DBE,
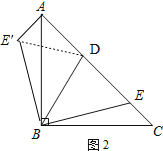
在△BDE′和△BDE中,
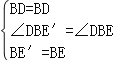 ,
,
∴△BDE′≌△BDE(SAS),
∴DE′=DE;
(2)解:以点B为旋转中心,将△EBC按顺时针方向旋转90°得到△E′BA(点C与点A重合,点E到点E′处),如图2,
∵∠ABC=90°,BA=BC,
∴∠BCE=∠BAD=45°,
∵△EBC按顺时针方向旋转90°得到△E′BA,
∴∠BAE′=∠BCE=45°,AE′=CE=2,
∴∠DAE′=∠BAD+∠BAE′=90°,
在Rt△DAE′中,∵DE′2=AD2+AE′2=42+22=20,
∴DE′=2![]() ,
,
由(1)的结论得DE=DE′=2![]() .
.


科目:初中数学 来源: 题型:
【题目】在课外实践活动中,甲、乙、丙、丁四个小组用投掷一元硬币的方法估算正面朝上的概率,其实验次数分别为10次、50次、100次,200次,其中实验相对科学的是( )
A.甲组 B.乙组 C.丙组 D.丁组
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC中,∠C=90°,∠B=30°,O为AB边中点,将△ABC绕点O逆时针旋转60°至△EDA位置,连接CD.
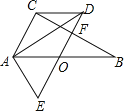
(1)求证:OD⊥BC;
(2)求证:四边形AODC为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OB平分∠CBA,CO平分∠ACB,且MN∥BC,设AB=12,BC=24,AC=18,则△AMN的周长为( )

A.30 B.33 C.36 D.39
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,∠ABC=90°,利用直尺和圆规,根据要求作图(不写作法,保留作图痕迹),并解决下面的问题.
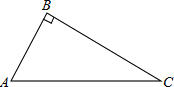
(1)作AC的垂直平分线,分别交AC、BC于点D、E;
(2)若AB=12,BE=5,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解中学生获取资讯的主要渠道,设置“A:手机,B:电视,C:网络,D:身边的人,E:其他”五个选项(五项中必选且只能选一项)的调查问卷,先随机抽取50名中学生进行该问卷调查,则该调查的方式是_______.(填普查或抽样调查)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某报亭老板以每份0.5元的价格从报社购进某种报纸500份,以每份0.8元的价格销售x份﹙x<500﹚,未销售完的报纸又以每份0.1元的价格由报社收回。这次买卖中该老板赚钱____元。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com