
【题目】如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE∥BD,过点D作ED∥AC,两线相交于点E. 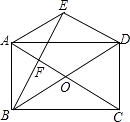
(1)求证:四边形AODE是菱形;
(2)连接BE,交AC于点F.若BE⊥ED于点E,求∠AOD的度数.
【答案】
(1)证明:∵AE∥BD,ED∥AC,
∴四边形AODE是平行四边形,
∵四边形ABCD是矩形,
∴OA=OC= ![]() AC,OB=OD=
AC,OB=OD= ![]() BD,AC=BD,
BD,AC=BD,
∴OA=OC=OD,
∴四边形AODE是菱形
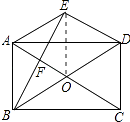
(2)解:连接OE,如图所示:
由(1)得:四边形AODE是菱形,
∴AE=OB=OA,
∵AE∥BD,
∴四边形AEOB是平行四边形,
∵BE⊥ED,ED∥AC,
∴BE⊥AC,
∴四边形AEOB是菱形,
∴AE=AB=OB,
∴AB=OB=OA,
∴△AOB是等边三角形,
∴∠AOB=60°,
∴∠AOD=180°﹣60°=120°.
【解析】(1)先证明四边形AODE是平行四边形,再由矩形的性质得出OA=OC=OD,即可得出四边形AODE是菱形;(2)连接OE,由菱形的性质得出AE=OB=OA,证明四边形AEOB是菱形,得出AB=OB=OA,证出△AOB是等边三角形,得出∠AOB=60°,再由平角的定义即可得出结果.
【考点精析】认真审题,首先需要了解矩形的性质(矩形的四个角都是直角,矩形的对角线相等).


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
【题目】日前一名男子报警称,在菲律宾南部发现印有马来西亚国旗的飞机残骸,怀疑是失联的马航MH370客机,马来西亚警方立即派出直升机前去查证.飞机在空中A点看见残骸C的俯角为20°,继续沿直线AE飞行16秒到达B点,看见残骸C的俯角为45°,已知飞机的飞行度为3150米/分. 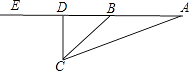
(参考数据:tan20°≈0.3,cos20°≈0.9,sin20°≈0.2)
(1)求残骸到直升机航线的垂直距离CD为多少米?
(2)在B点时,机组人员接到总指挥部电话,8分钟后该海域将迎来比较大的风浪,为了能及时观察取证,机组人员决定飞行到D点立即空投设备,将残骸抓回机舱(忽略风速对设备的影响),己知设备在空中的降落与上升速度均为700米/分.设备抓取残骸本身需要6分钟,请问能否在风浪来临前将残骸抓回机舱?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对于实数a,符号[a]表示不大于a的最大整数,例如:[4.7]=4,[﹣π]=﹣4,[3]=3,如果[ ![]() +1]=﹣5,则x的取值范围为 .
+1]=﹣5,则x的取值范围为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点O是AC边上的一动点,过O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F. 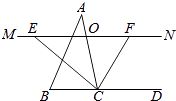
(1)求证:EO=FO;
(2)当CE=12,CF=10时,求CO的长;
(3)当O点运动到何处时,四边形AECF是矩形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大型超市从生产基地购进一批水果,运输过程中质量损失10%,假设不计超市其它费用,如果超市要想至少获得20%的利润,那么这种水果的售价在进价的基础上应至少提高( )
A.40%
B.33.4%
C.33.3%
D.30%
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com