
【题目】已知命题:“P 是等边△ABC 内的一点,若 P 到三边的距离相等,则 PA=PB=PC.”
(1)写出它的逆命题.判断其逆命题成立吗?若成立,请给出证明.
(2)进一步证明:点 P 到等边△ABC 各边的距离之和为定值.
【答案】
(1)解:逆命题:P 是等边三角形 ABC内的一点,若PA=PB=PC,则P到三边的距离相等. 该逆命题成立.
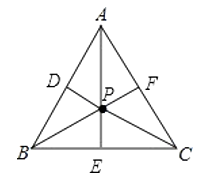
已知:如图:P是等边△ABC内的一点,若PA=PB=PC,PD⊥AB于D,PF⊥AC于F,PE⊥BC于E,
求证:PD=PE=PF.
证明:∵PA=PB,
∴P 在 AB 的垂直平分线上,
∵AC=BC,
∴C 在 AB 的垂直平分线上,
∴CP 是 AB 的垂直平分线,
∴CP 平分∠ACB,
同理,BP 平分∠ABC,AP 平分∠BAC,
∴P 是△ABC 三个角的角平分线的交点,
又∵PD⊥AB,PF⊥AC,PE⊥BC,
∴PD=PE=PF.
(2)证明:设AB边上的高为h,
∵AB=BC=AC 且 S△ABC=S△ABP +S△PBC +S△APC,
∴![]() AB.h=
AB.h=![]() AB.PD+
AB.PD+![]() BC.PE+
BC.PE+![]() AC.PF,
AC.PF,
∴h=PD+PE+PF,
∴点P到等边△ABC各边的距离之和为定值.定值为该三角形任意边上的高长.
【解析】(1)由垂直平分线的判定得出点P、点C均在 AB 的垂直平分线上,即CP 是 AB 的垂直平分线;再根据等腰三角形的性质得出CP 平分∠ACB;
同理,BP 平分∠ABC,AP 平分∠BAC,根据角平分线的性质得出PD=PE=PF.
(2)设AB边上的高为h,由 S△ABC=S△ABP +S△PBC +S△APC,从而得出h=PD+PE+PF,即为定值.
【考点精析】根据题目的已知条件,利用线段垂直平分线的判定和三角形的面积的相关知识可以得到问题的答案,需要掌握和一条线段两个端点距离相等的点,在这条线段的垂直平分线上;三角形的面积=1/2×底×高.


科目:初中数学 来源: 题型:
【题目】2016年10月1日,重庆四大景区共接待游客约518 000人,这个数可用科学记数法表示为( )
A.0.518×104
B.5.18×105
C.51.8×106
D.518×103
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张老师计划到超市购买甲种文具100个,他到超市后发现还有乙种文具可供选择.如果调整文具的购买品种,每减少购买1个甲种文具,需增加购买2个乙种文具.设购买x个甲种文具时,需购买y个乙种文具.
(1)①当减少购买1个甲种文具时,x= ,y= ;②求y与x之间的函数表达式.
(2)已知甲种文具每个5元,乙种文具每个3元,张老师购买这两种文具共用去540元.甲、乙两种文具各购买了多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD∥AB,∠ABC,∠BCD 的角平分线交 AD 于 E 点,且 E 在 AD 上,CE 交 BA 的延长线于 F 点.
(1)试问 BE 与 CF 互相垂直吗?若垂直,请说明理由;
(2)若 CD=3,AB=4,求 BC 的长 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】粗心的小红在计算n边形的内角和时,少加了一个内角,求得的内角和是2040°,则这个多边形的边数n和这个内角分别是( )
A.11和60°
B.11和120°
C.12和60°
D.14和120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举办了一次成语知识竞赛,满分10分,学生得分均为整数,成绩达到6分及6分以上为合格,达到9分或10分为优秀.这次竞赛中甲、乙两组学生成绩分布的折线统计图和成绩统计分析表如图所示.
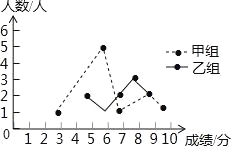
(1)求出下列成绩统计分析表中![]() 的值;
的值;
(2)小英同学说:“这次竞赛我得了7分,在我们小组中排名属中游略上!”观察上面表格判断,小英是甲、乙哪个组的学生;
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组,但乙组同学不同意甲组同学的说法,认为他们的成绩要好于甲组.请你给出两条支持乙组同学观点的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,最适合采用全面调查(普查)的是( )
A.某班学生对国家“一带一路”战略的知晓率
B.鞋厂检测生产的鞋底能承受的弯曲次数
C.检测某城市的空气质量
D.了解电视栏目《朗读者》的收视率
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com