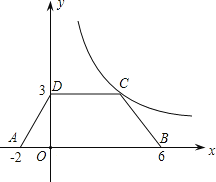
【题目】如图，等腰梯形ABCD放置在平面坐标系中，已知A（﹣2，0）、B（6，0）、D（0，3），反比例函数的图象经过点C．

（1）求点C的坐标和反比例函数的解析式；

（2）将等腰梯形ABCD向上平移2个单位后，问点B是否落在双曲线上？

参考答案：

【答案】（1）y=（2）恰好落在双曲线上

【解析】（1）过点C作CE⊥AB于点E，

∵四边形ABCD是等腰梯形，

∴AD=BC，DO=CE，

∴△AOD≌△BEC，∴AO=BE=2，

∵BO=6，∴DC=OE=4，

∴C（4，3）；

设反比例函数的解析式y=（k≠0），

根据题意得：3=，

解得k=12；

∴反比例函数的解析式y=；

（2）将等腰梯形ABCD向上平移2个单位后得到梯形A′B′C′D′得点B′（6，2），

故当x=6时，y==2，即点B′恰好落在双曲线上．

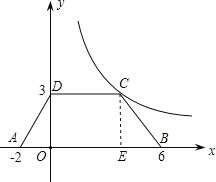
（1）C点的纵坐标与D的纵坐标相同，过点C作CE⊥AB于点E，则△AOD≌△BEC，即可求得BE的长度，则OE的长度即可求得，即可求得C的横坐标，然后利用待定系数法即可求得反比例函数的解析式；

（2）将等腰梯形ABCD向上平移2个单位后，点B向上平移2个单位长度得到的点的坐标即可得到，代入函数解析式判断即可．

关闭