练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】下列命题中，属于假命题的是（　　）

    A. 有一个锐角相等的两个直角三角形一定相似

    B. 对角线相等的菱形是正方形

    C. 抛物线y=x2﹣20x+17的开口向上

    D. 在一次抛掷图钉的试验中，若钉尖朝上的频率为，钉尖朝下的概率为

    【答案】D

    【解析】

    根据相似三角形的判定定理、正方形的判定定理、二次函数的性质以及概率的意义判断即可．

    有一个锐角相等的两个直角三角形一定相似，A是真命题；

    对角线相等的菱形是正方形，B是真命题；

    ∵a=1＞0，∴抛物线y=x2﹣20x+17的开口向上，C是真命题；

    ∵在抛掷图钉的试验中，不只是钉尖朝上和钉尖朝下两种情况，∴在一次抛掷图钉的试验中，若钉尖朝上的频率为，钉尖朝下的概率不确定，D是假命题．

    故选D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

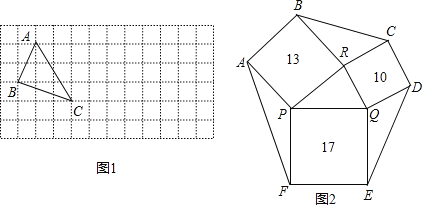
    【题目】现场学习：在△ABC中，AB、BC、AC三边的长分别为、、，求这个三角形的面积．小华同学在解答这道题时，先画一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处），如图1所示．这样不需求△ABC的高，而借用网格就能计算出它的面积．这种方法叫做构图法．

    （1）△ABC的面积为：　_________　；

    （2）若△DEF三边的长分别为、、，请在图1的正方形网格中画出相应的△DEF，并利用构图法求出它的面积；

    （3）如图2，一个六边形的花坛被分割成7个部分，其中正方形PRBA，RQDC，QPFE的面积分别为13，10，17，且△PQR、△BCR、△DEQ、△AFP的面积相等，求六边形花坛ABCDEF的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，P是半径为cm的⊙O外一点，PA，PB分别和⊙O切于点A，B，PA=PB=3cm，∠APB=60°，C是弧AB上一点，过C作⊙O的切线交PA，PB于点D，E．

    （1）求△PDE的周长；

    （2）若DE=cm，求图中阴影部分的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面真角坐标系中， 有、两点， 若在轴上取一点， 使点到点和点的距离之和最小，则点的坐标是__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，Rt△OAB如图所示放置在平面直角坐标系中，直角边OA与x轴重合，∠OAB=90°，OA=4，AB=2，把Rt△OAB绕点O逆针旋转90°，点B旋转到点C的位置，一条抛物找正好经过点O，C，A三点．

    （1）求该抛物线的解析式；

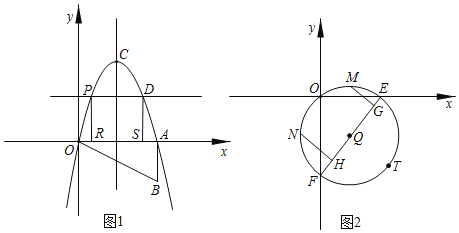
    （2）在x轴上方的抛物线上有一动点P，过点P作x轴的平行线交抛物线于点D，分别过点P，点D作x轴的垂线，交x轴于R，S两点，问：四边形PRSD的周长是否有最大值？如果有，请求出最值，并写出解答过程；如果没有，请说明理由．

    （3）如图2，把点B向下平移两个单位得到点T，过O，T两点作⊙Q交x轴，y轴于E，F两点，若M、N分别为弧、的中点，作MG⊥EF，NH⊥EF，垂足为G、H，试求MG+NH的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中,A(1,0),B(0,2),C(-4,2),若以A,B,C,D为顶点的四边形是平行四边形,则点D的坐标为________________。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校要从甲、乙两名同学中挑选一人参加创新能力大赛，在最近的五次选拔测试中， 他俩的成绩分别如下表，请根据表中数据解答下列问题：

    第 1 次

    第 2 次

    第 3 次

    第 4 次

    第 5 次

    平均分

    众数

    中位数

    方差

    甲

    60 分

    75 分

    100 分

    90 分

    75 分

    80 分

    75 分

    75 分

    190

    乙

    70 分

    90 分

    100 分

    80 分

    80 分

    80 分

    80 分

    （1）把表格补充完整：

    （2）在这五次测试中，成绩比较稳定的同学是多少；若将 80 分以上（含 80 分） 的成绩视为优秀，则甲、乙两名同学在这五次测试中的优秀率分别是多少；

    （3）历届比赛表明，成绩达到80分以上（含 80分）就很可能获奖，成绩达到 90分以上（含90分）就很可能获得一等奖，那么你认为选谁参加比赛比较合适？说明你的理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一次函数y=kx+b（k、b为常数，k≠0）的图象与x轴、y轴分别交于A、B两点，且与反比例函数y=（n为常数，且n≠0）的图象在第二象限交于点C．CD⊥x轴，垂足为D，若OB=2OA=3OD=12．

    （1）求一次函数与反比例函数的解析式；

    （2）记两函数图象的另一个交点为E，求△CDE的面积；

    （3）直接写出不等式kx+b≤的解集．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将一张矩形纸板按图中虚线裁剪成九块，其中有两块是边长都为的大正方形，两块是边长都为的小正方形，五块是长为、宽为的全等小矩形，且> ．（以上长度单位：cm）

    （1）观察图形，可以发现代数式可以因式分解为 ；

    （2）若每块小矩形的面积为10，四个正方形的面积和为58，试求图中所有裁剪线（虚线部分）长之和．

    查看答案和解析>>

    同步练习册答案