
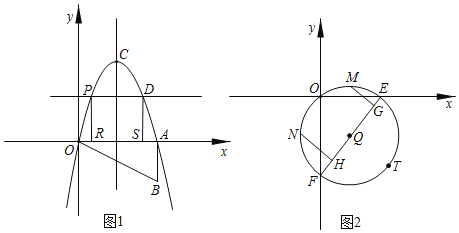
【题目】如图,Rt△OAB如图所示放置在平面直角坐标系中,直角边OA与x轴重合,∠OAB=90°,OA=4,AB=2,把Rt△OAB绕点O逆针旋转90°,点B旋转到点C的位置,一条抛物找正好经过点O,C,A三点.
(1)求该抛物线的解析式;
(2)在x轴上方的抛物线上有一动点P,过点P作x轴的平行线交抛物线于点D,分别过点P,点D作x轴的垂线,交x轴于R,S两点,问:四边形PRSD的周长是否有最大值?如果有,请求出最值,并写出解答过程;如果没有,请说明理由.
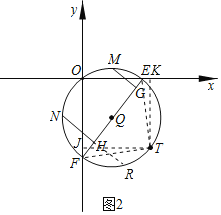
(3)如图2,把点B向下平移两个单位得到点T,过O,T两点作⊙Q交x轴,y轴于E,F两点,若M、N分别为弧![]() 、
、![]() 的中点,作MG⊥EF,NH⊥EF,垂足为G、H,试求MG+NH的值.
的中点,作MG⊥EF,NH⊥EF,垂足为G、H,试求MG+NH的值.
【答案】(1)y=-x2+4x;(2)当a=1时,矩形PEFM的周长有最大值10;(3)MG+NH=4.
【解析】
(1)根据旋转变换的性质求出点C的坐标,利用待定系数法求出抛物线的解析式;
(2)设点P的坐标为P(a,-a2+4a),根据抛物线的对称性求出RS,根据二次函数的性质计算;
(3)作TK⊥x轴于K,TJ⊥y轴于J,连接TF,TE,延长NH交⊙Q于R,证明△ETK≌△FTJ,根据全等三角形的性质得到EK=FJ,得到OE+OF=8,根据垂径定理得到NH=NR=![]() OF,计算即可.
OF,计算即可.
解:(1)设y=ax2+bx+c,
∵OA=4,AB=2,
∴点A的坐标为(4,0),点B的坐标为(4,-2),
△AOB绕点O逆时针旋转90°,点B旋转到点C的位置,
∴点C的坐标为(2,4),
则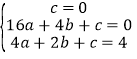
解得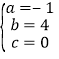 .
.
所以抛物线的解析式为y=-x2+4x;
(2)有最大值.
理由如下:设点P的坐标为P(a,-a2+4a),PR=DS=-a2+4a,
由抛物线的对称性知OR=AS,RS=PD=4-2a,
矩形PRSD的周长=2[4-2a+(-a2+4a)]=-2(a-1)2+10,
所以当a=1时,矩形PEFM的周长有最大值10;
(3)作TK⊥x轴于K,TJ⊥y轴于J,连接TF,TE,延长NH交⊙Q于R,
由题意得,点T的坐标为(4,-4,),即TJ=TK=4,
∴点T在∠EOF的平分线上,
∴![]() =
=![]()
∴TE=TF,
在Rt△TKE和Rt△TJF中,
![]() ,
,
∴△ETK≌△FTJ(HL),
∴EK=FJ,∠EOF=∠KTJ=90°,
∴OE+OF=OK-EK+OJ+FJ=OJ+OK=8,
∴EF为⊙Q的直径,
∴![]() =
=![]() ,
,
∵N为![]() 的中点,
的中点,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴NR=OF,
∴NH=NR=![]() OF,
OF,
同理MG=![]() OE,
OE,
∴MG+NH=![]() (OE+OF)=
(OE+OF)=![]() ×8=4.
×8=4.


科目:初中数学 来源: 题型:
【题目】(问题解决)
一节数学课上,老师提出了这样一个问题:如图1,点P是正方形ABCD内一点,PA=1,PB=2,PC=3.你能求出∠APB的度数吗?
小明通过观察、分析、思考,形成了如下思路:
思路一:将△BPC绕点B逆时针旋转90°,得到△BP′A,连接PP′,求出∠APB的度数;
思路二:将△APB绕点B顺时针旋转90°,得到△CP'B,连接PP′,求出∠APB的度数.
请参考小明的思路,任选一种写出完整的解答过程.
(类比探究)
如图2,若点P是正方形ABCD外一点,PA=3,PB=1,PC=![]() ,求∠APB的度数.
,求∠APB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
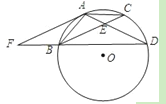
【题目】如图,点A,B,C,D在⊙O上,AB=AC,AD与BC相交于点E,AE=![]() ED,延长DB到点F,使FB=
ED,延长DB到点F,使FB=![]() BD,连接AF.
BD,连接AF.
(1)证明:△BDE∽△FDA;
(2)试判断直线AF与⊙O的位置关系,并给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
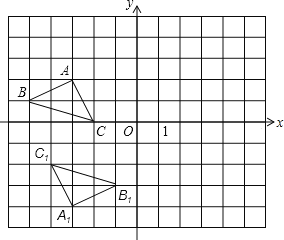
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(1,1),B(4,1),C(3,3).
(1)将△ABC向下平移5个单位后得到△A1B1C1,请画出△A1B1C1;
(2)将△ABC绕原点O逆时针旋转90°后得到△A2B2C2,请画出△A2B2C2;
(3)判断以O,A1,B为顶点的三角形的形状.(无须说明理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,属于假命题的是( )
A. 有一个锐角相等的两个直角三角形一定相似
B. 对角线相等的菱形是正方形
C. 抛物线y=x2﹣20x+17的开口向上
D. 在一次抛掷图钉的试验中,若钉尖朝上的频率为![]() ,钉尖朝下的概率为
,钉尖朝下的概率为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,每个小正方形网格的边长为1,![]() 和
和![]() 关于点
关于点![]() 成中心对称.
成中心对称.
(1)画出对称中心![]() ,并写出点
,并写出点![]() 的坐标______.
的坐标______.
(2)画出![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 后的
后的![]() ;连接
;连接![]() ,可求得线段
,可求得线段![]() 长为______.
长为______.
(3)画出![]() 与关于点
与关于点![]() 成中心对称的
成中心对称的![]() ;连接
;连接![]() 、
、![]() ,则四边形
,则四边形![]() 是______;(填属于哪一种特殊四边形),它的面积是______.
是______;(填属于哪一种特殊四边形),它的面积是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB=8cm,小红在作线段AB的垂直平分线时操作如下:分别以A和B为圆心,5cm的长为半径画弧,两弧相交于C、D,则直线CD即为所求,根据此种作图方法所得到的四边形ADBC的面积是( )
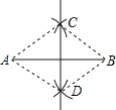
A.12cm2B.24cm2C.36cm2D.48cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若干个全等的正五边形排成环状,图中所示的是前3个正五边形,要完成这一圆环还需正五边形的个数为( )
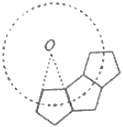
A. 10 B. 9 C. 8 D. 7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com