
【题目】(问题解决)
一节数学课上,老师提出了这样一个问题:如图1,点P是正方形ABCD内一点,PA=1,PB=2,PC=3.你能求出∠APB的度数吗?
小明通过观察、分析、思考,形成了如下思路:
思路一:将△BPC绕点B逆时针旋转90°,得到△BP′A,连接PP′,求出∠APB的度数;
思路二:将△APB绕点B顺时针旋转90°,得到△CP'B,连接PP′,求出∠APB的度数.
请参考小明的思路,任选一种写出完整的解答过程.
(类比探究)
如图2,若点P是正方形ABCD外一点,PA=3,PB=1,PC=![]() ,求∠APB的度数.
,求∠APB的度数.

【答案】(1)见解析;(2)见解析.
【解析】
(1)先利用旋转求出∠PBP'=90°,BP'=BP=2,AP'=CP=3,利用勾股定理求出PP',进而判断出△APP'是直角三角形,得出∠APP'=90°,即可得出结论;
(2)同(1)的思路一的方法即可得出结论.
(1)如图1,
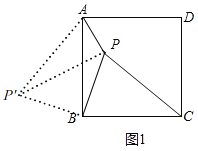
将△BPC绕点B逆时针旋转90°,得到△BP′A,连接PP′,
∴△ABP'≌△CBP,
∴∠PBP'=90°,BP'=BP=2,AP'=CP=3,
在Rt△PBP'中,BP=BP'=2,
∴∠BPP'=45°,根据勾股定理得,PP'=![]() BP=2
BP=2![]() ,
,
∵AP=1,
∴AP2+PP'2=1+8=9,
∵AP'2=32=9,
∴AP2+PP'2=AP'2,
∴△APP'是直角三角形,且∠APP'=90°,
∴∠APB=∠APP'+∠BPP'=90°+45°=135°;
(2)如图2,
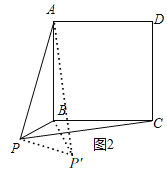
将△BPC绕点B逆时针旋转90°,得到△BP′A,连接PP′,
∴△ABP'≌△CBP,
∴∠PBP'=90°,BP'=BP=1,AP'=CP=![]() ,
,
在Rt△PBP'中,BP=BP'=1,
∴∠BPP'=45°,根据勾股定理得,PP'=![]() BP=
BP=![]() ,
,
∵AP=3,
∴AP2+PP'2=9+2=11,
∵AP'2=(![]() )2=11,
)2=11,
∴AP2+PP'2=AP'2,
∴△APP'是直角三角形,且∠APP'=90°,
∴∠APB=∠APP'﹣∠BPP'=90°﹣45°=45°.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
【题目】如图1,将一块含有![]() 角的三角板放置在一条直线上,
角的三角板放置在一条直线上,![]() 边与直线
边与直线![]() 重合,
重合,![]() 边的垂直平分线与边
边的垂直平分线与边![]() 分别交于
分别交于![]() 两点,连接
两点,连接![]() .
.


(1) ![]() 是 三角形;
是 三角形;
(2)直线![]() 上有一动点
上有一动点![]() (不与点
(不与点![]() 重合) ,连接
重合) ,连接![]() 并把
并把![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 到
到![]() ,连接
,连接![]() .当点
.当点![]() 在图2所示的位置时,证明
在图2所示的位置时,证明![]() .我们可以用
.我们可以用![]() 来证明
来证明![]() ,从而得到
,从而得到![]() .当点
.当点![]() 移动到图3所示的位置时,结论是否依然成立?若成立,请你写出证明过程;若不成立,请你说明理由.
移动到图3所示的位置时,结论是否依然成立?若成立,请你写出证明过程;若不成立,请你说明理由.
(3)当点![]() 在
在![]() 边上移动时(不与点
边上移动时(不与点![]() 重合),
重合),![]() 周长的最小值是 .
周长的最小值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为美化校园,计划对面积为1800m2的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为400 m2区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积分别是多少m2?
(2)若学校每天需付给甲队的绿化费用是0.4万元,乙队为0.25万元,要使这次的绿化总费用不超过8万元,至少应安排甲队工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则OF的长度是( )

A. 3cm B. ![]() cm C. 2.5cm D.
cm C. 2.5cm D. ![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
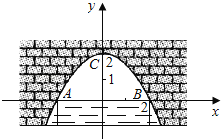
【题目】图中是抛物线形拱桥,当拱顶离水面2m时,水面宽4m,建立如图所示的平面直角坐标系:
(1)求拱桥所在抛物线的解析式;
(2)当水面下降1m时,则水面的宽度为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学重要的著作之一,奠定了中国传统数学的基本框架.其中第九卷《勾股》主要讲述了以测量问题为中心的直角 三角形三边互求,之中记载了一道有趣的“折竹抵地”问题:
“今有竹高一丈,末折抵地,去本四尺,问折者高几何?”
译文:“一根竹子,原高一丈,一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部4尺远,则折断后的竹子高度为多少尺?”(备注:1丈=10尺)
如果设竹梢到折断处的长度为![]() 尺,那么折断处到竹子的根部用含
尺,那么折断处到竹子的根部用含![]() 的代数式可表示为__________尺,根据题意,可列方程为_______________________.
的代数式可表示为__________尺,根据题意,可列方程为_______________________.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△OAB的边长为2,点B在x轴上,反比例函数的图象经过A点,将△OAB绕点O顺时针旋转α(0°<α<360°),使点A落在双曲线上,则α=________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(5,3),B(6,5),C(4,6).
(1)画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标.
(2)将△A1B1C1向左平移6个单位,再向上平移5个单位,画出平移后得到的△A2B2C2,并写出点B2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①所示是边长为![]() 的大正方形中有一个边长为
的大正方形中有一个边长为![]() 的小正方形.图②是由图①中阴影部分拼成的一个长方形.
的小正方形.图②是由图①中阴影部分拼成的一个长方形.

(1)设图①中阴影部分的面积为![]() ,图②中阴影部分的面积为
,图②中阴影部分的面积为![]() ,请用含
,请用含![]() 的式子表示:
的式子表示:![]() ,
,![]() ;(不必化简)
;(不必化简)
(2)以上结果可以验证的乘法公式是 ;
(3)利用(2)中得到的公式,计算:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com