练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A(5，3)，B(6，5)，C(4，6)．

    (1)画出△ABC关于x轴对称的△A1B1C1，并写出点A1的坐标.

    (2)将△A1B1C1向左平移6个单位，再向上平移5个单位，画出平移后得到的△A2B2C2，并写出点B2的坐标．

    【答案】（1）点A1的坐标（5，3）；（2）点B2的坐标（0，0）．图见解析

    【解析】

    首先确定A、B、C三点关于x轴的对称点，然后再连接即可得到△A1B1C1，然后再确定A1、B1、C1三点向左平移6个单位，再向上平移5个单位后的对应点位置，再连接即可得到△A2B2C2．

    （1）如图所示：△A1B1C1为所求，点A1的坐标（5，3）；

    （2）△A2B2C2为所求，点B2的坐标（0，0）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知：如图，在平面直角坐标系中，△ABC是直角三角形，∠ACB=90°，点A、C的坐标分别为A（﹣3，0），C（1，0），．

    （1）求过点A、B的直线的函数表达式；

    （2）在x轴上找一点D，连接DB，使得△ADB与△ABC相似（不包括全等），并求点D的坐标；

    （3）在（2）的条件下，如P、Q分别是AB和AD上的动点，连接PQ，设AP=DQ=m，问是否存在这样的m使得以点A、P、Q为顶点的三角形与△ADB相似？如存在，请求出m的值；如不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（问题解决）

    一节数学课上，老师提出了这样一个问题：如图1，点P是正方形ABCD内一点，PA=1，PB=2，PC=3．你能求出∠APB的度数吗？

    小明通过观察、分析、思考，形成了如下思路：

    思路一：将△BPC绕点B逆时针旋转90°，得到△BP′A，连接PP′，求出∠APB的度数；

    思路二：将△APB绕点B顺时针旋转90°，得到△CP'B，连接PP′，求出∠APB的度数．

    请参考小明的思路，任选一种写出完整的解答过程．

    （类比探究）

    如图2，若点P是正方形ABCD外一点，PA=3，PB=1，PC=，求∠APB的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在探究三角形内角和等于180°的证明过程时，小明同学通过认真思考后认为，可以通过剪拼的方法将一个角剪下来，然后把这个角进行平移，从而实现把三角形的三个内角转移到一个平角中去，如图所示：

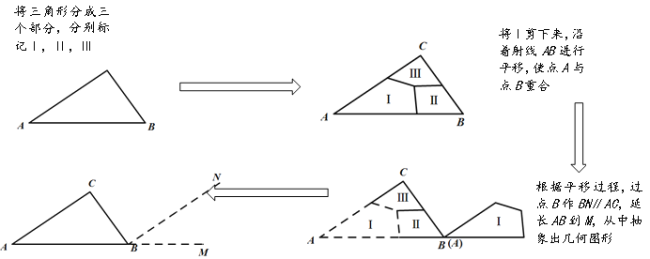
    （1）小明同学根据剪拼的过程，抽象出几何图形；并进行了推理证明，请你帮助小明完成

    证明过程．

    证明：过点B作BN//AC,延长AB到M

    ∵

    ∴

    ∵

    ∴

    （2）小军仿照小明的方法将三角形的三个内角都进行了移动，也将三个内角转移到一个平 角中去，只不过平角的顶点放到了AB边上，如图所示：请你仿照小明的证明过程，抽象出几何图形再进行证明．

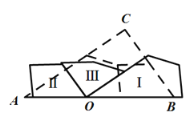
    （3）小兰的方法和小明以及小军的方法都不相同，她将三角形三个内角分别沿某一条直线翻折，一共进行了三次尝试，如图所示：

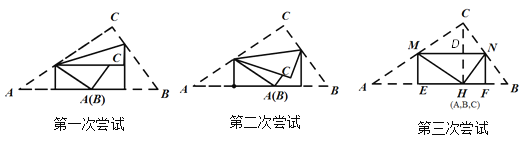
    小兰第三次成功的关键是什么，请你写出证明思路．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知平行四边形OBDC的对角线相交于点E，其中O（0，0），B（3，4），C（m，0），反比例函数y=（k≠0）的图象经过点B．

    （1）求反比例函数的解析式；

    （2）若点E恰好落在反比例函数y=上，求平行四边形OBDC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图：直线y=x与反比例函数y=（k＞0）的图象在第一象限内交于点A（2，m）．

    （1）求m、k的值；

    （2）点B在y轴负半轴上，若△AOB的面积为2，求AB所在直线的函数表达式；

    （3）将△AOB沿直线AB向上平移，平移后A、O、B的对应点分别为A'、O'、B'，当点O'恰好落在反比例函数y=的图象上时，求点A'的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

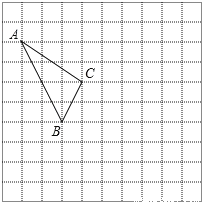
    【题目】在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形（顶点是网格线的交点的三角形）ABC的顶点A，C的坐标分别为（﹣4，5），（﹣1，3）．

    （1）请在如图所示的网格平面内作出平面直角坐标系；

    （2）写出点B的坐标；

    （3）将△ABC向右平移5个单位长度，向下平移2个单位长度，画出平移后的图形△A′B′C′；

    （4）计算△A′B′C′的面积﹒

    （5）在x轴上存在一点P，使PA+PC最小，直接写出点P的坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD的四个顶点分别在反比例函数y=与y=（x＞0，0＜m＜n）的图象上，对角线BD∥y轴，且BD⊥AC于点P．已知点B的横坐标为4．

    （1）当m=4，n=20时．

    ①若点P的纵坐标为2，求直线AB的函数表达式．

    ②若点P是BD的中点，试判断四边形ABCD的形状，并说明理由．

    （2）四边形ABCD能否成为正方形？若能，求此时m，n之间的数量关系；若不能，试说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，等边△ABC中，AD为BC边上的高，点M、N分别在AD、AC上，且AM＝CN，连BM、BN，当BM+BN最小时，∠MBN＝_____度．

    查看答案和解析>>

    同步练习册答案