Question

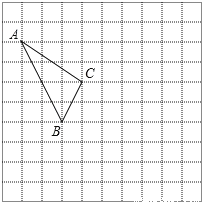
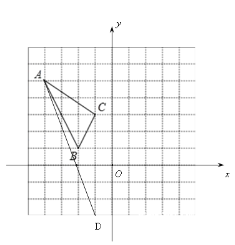
【题目】在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形（顶点是网格线的交点的三角形）ABC的顶点A，C的坐标分别为（﹣4，5），（﹣1，3）．

（1）请在如图所示的网格平面内作出平面直角坐标系；

（2）写出点B的坐标；

（3）将△ABC向右平移5个单位长度，向下平移2个单位长度，画出平移后的图形△A′B′C′；

（4）计算△A′B′C′的面积﹒

（5）在x轴上存在一点P，使PA+PC最小，直接写出点P的坐标.

Answer 1

【答案】(1)详见解析;(2)B(-2,1);(3)详见解析;(4)4;(5)P(,0).

【解析】

(1)直接利用已知点位置得出x,y轴的位置；

(2)利用平面直角坐标系得出B点坐标即可；

(3)直接利用平移的性质得出对应点位置进而得出答案；

(4)利用△A′B′C′所在矩形形面积减去周围三角形面积进而得出答案．

(5)作C关于x轴的对称点D,连接AD交x轴一点就为所求点.

(1)如图所示,∵点A的坐标为（﹣4,5）,

∴在A点y轴向右平移4个单位,x轴向下平移5个单位得到即可；

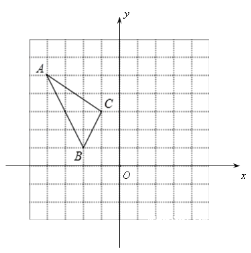
(2)B（﹣2,1）；

(3)如图所示：△A′B′C′即为所求；

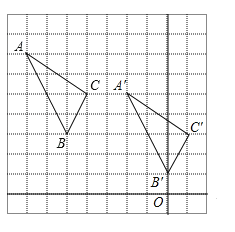
(4)△A′B′C′的面积为：3×4﹣×3×2﹣×1×2﹣×2×4=4．

(5)作点C关于x轴的对称点D(-1,-3),连接AD交x轴于一点,该点为所求点.

设直线AD:y=kx+b,将A(-4,5),D(-1,-3)代入

解得: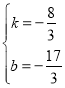

直线AD:

令y=0,则x=

∴P点坐标为(,0)