【题目】已知关于
的一元二次方程
．
若该方程有实数根，求
的取值范围．
若该方程一个根为
，求方程的另一个根．
【答案】（1）
的取值范围为
且
；（2）方程的另一个根为
．
【解析】
（1）根据一元二次方程的定义结合根的判别式即可得出关于a的一元一次不等式组，解之即可得出结论；
（2）将x=﹣1代入原方程求出a的值，设方程的另一个根为m，将a代入原方程结合根与系数的关系即可得出关于m的一元一次方程，解之即可得出结论．
（1）∵关于x的一元二次方程（a﹣5）x2﹣4x﹣1=0有实数根，∴
，解得：a≥1且a≠5，∴a的取值范围为a≥1且a≠5．
（2）∵方程一个根为﹣1，∴（a﹣5）×（﹣1）2﹣4×（﹣1）﹣1=0，解得：a=2．
当a=2时，原方程为3x2+4x+1=0，设方程的另一个根为m，由根与系数的关系得：﹣m=
，解得：m=﹣，∴方程的另一个根为﹣．
学业测评一课一测系列答案
小学课时作业全通练案系列答案科目：初中数学 来源： 题型：
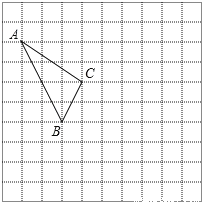
【题目】在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形（顶点是网格线的交点的三角形）ABC的顶点A，C的坐标分别为（﹣4，5），（﹣1，3）．
（1）请在如图所示的网格平面内作出平面直角坐标系；
（2）写出点B的坐标；
（3）将△ABC向右平移5个单位长度，向下平移2个单位长度，画出平移后的图形△A′B′C′；
（4）计算△A′B′C′的面积﹒
（5）在x轴上存在一点P，使PA+PC最小，直接写出点P的坐标.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知AB是⊙O的直径，PB是⊙O的切线，C是⊙O上的点，AC∥OP，M是直径AB上的动点，A与直线CM上的点连线距离的最小值为d，B与直线CM上的点连线距离的最小值为f．
（1）求证：PC是⊙O的切线；
（2）设OP=
AC，求∠CPO的正弦值；
（3）设AC=9，AB=15，求d+f的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，等边△ABC中，AD为BC边上的高，点M、N分别在AD、AC上，且AM＝CN，连BM、BN，当BM+BN最小时，∠MBN＝_____度．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在5×5的正方形网格中，从在格点上的点A，B，C，D中任取三点，所构成的三角形恰好是直角三角形的个数为（ ）
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某家具商场计划购进某种餐桌、餐椅进行销售，有关信息如下表：
原进价（元/张） | 零售价（元/张） | 成套售价（元/套） | |
餐桌 | a | 270 | 500 |
餐椅 | b | 70 |
若购进3张餐桌18张餐椅需要1170元；若购进5张餐桌25张餐椅需要1750元．
（1）求表中a，b的值；
（2）若该商场购进餐椅的数量是餐桌数量的5倍还多20张，且餐桌和餐椅的总数量不超过200张．该商场计划将全部餐桌配套销售（一张餐桌和四张餐椅配成一套），其余餐椅以零售方式销售．设购进餐桌的数量为x（张），总利润为W（元），求W关于x的函数关系式，并求出总利润最大时的进货方案．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】随着“互联网+”时代的到来，一种新型打车方式受到大众欢迎，该打车方式的总费用由里程费和耗时费组成，其中里程费按x元/公里计算，耗时费按y元/分钟计算（总费用不足9元按9元计价）．小明、小刚两人用该打车方式出行，按上述计价规则，其打车总费用、行驶里程数与打车时间如表：
时间（分钟） | 里程数（公里） | 车费（元） | |
小明 | 8 | 8 | 12 |
小刚 | 12 | 10 | 16 |
（1）求x，y的值；
（2）如果小华也用该打车方式，打车行驶了11公里，用了14分钟，那么小华的打车总费用为多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】你吃过拉面吗？实际上在做拉面的过程中就渗透着数学知识：一定体积的面团做成拉面，面条的总长度
是面条的粗细（横截面积）
的反比例函数，其图象如图所示．
写出
与
的函数关系式：________．
当面条粗
时，面条总长度是________
．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
