Question

【题目】如图，等边△ABC中，AD为BC边上的高，点M、N分别在AD、AC上，且AM＝CN，连BM、BN，当BM+BN最小时，∠MBN＝_____度．

Answer 1

【答案】30．

【解析】

如图1中，作CH⊥BC，使得CH＝BC，连接NH，BH．证明△ABM≌△CHN（SAS），推出BM＝HN，由BN+HN≥BH，可知B，N，H共线时，BM+BN＝NH+BN的值最小，求出此时∠MBN即可解决问题．

解：如图1中，作CH⊥BC，使得CH＝BC，连接NH，BH．

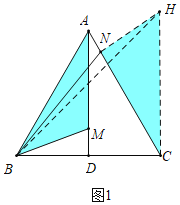
∵△ABC是等边三角形，AD⊥BC，CH⊥BC，

∴∠DAC＝∠DAB＝30°，AD∥CH，

∴∠HCN＝∠CAD＝∠BAM＝30°，

∵AM＝CN，AB＝BC＝CH，

∴△ABM≌△CHN（SAS），

∴BM＝HN，

∵BN+HN≥BH，

∴B，N，H共线时，BM+BN＝NH+BN的值最小，

如图2中，当B，N，H共线时，

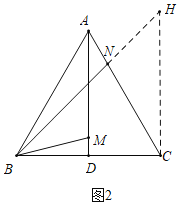
∵△ABM≌△CHN，

∴∠ABM＝∠CHB＝∠CBH＝45°，

∵∠ABD＝60°，

∴∠DBM＝15°，

∴∠MBN＝45°﹣15°＝30°，

∴当BM+BN的值最小时，∠MBN＝30°，

故答案为30．