Question

【题目】在探究三角形内角和等于180°的证明过程时，小明同学通过认真思考后认为，可以通过剪拼的方法将一个角剪下来，然后把这个角进行平移，从而实现把三角形的三个内角转移到一个平角中去，如图所示：

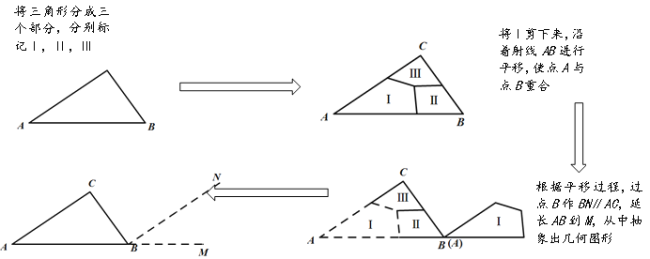
（1）小明同学根据剪拼的过程，抽象出几何图形；并进行了推理证明，请你帮助小明完成

证明过程．

证明：过点B作BN//AC,延长AB到M

∵

∴

∵

∴

（2）小军仿照小明的方法将三角形的三个内角都进行了移动，也将三个内角转移到一个平 角中去，只不过平角的顶点放到了AB边上，如图所示：请你仿照小明的证明过程，抽象出几何图形再进行证明．

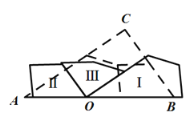
（3）小兰的方法和小明以及小军的方法都不相同，她将三角形三个内角分别沿某一条直线翻折，一共进行了三次尝试，如图所示：

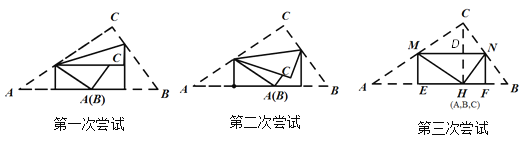
小兰第三次成功的关键是什么，请你写出证明思路．

Answer 1

【答案】（1）见解析；（2）见解析；（3）见解析.

【解析】

（1）根据平行线的性质即可作答；

（2）根据平行线的性质结合平角的性质即可证明；

（3）根据垂直的定义以及翻折的性质得，，，从而证得结论.

(1)两直线平行，同位角相等； 两直线平行，内错角相等．

(2)

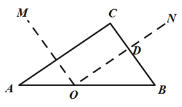
证明：Ｏ是线段AB上的一点，过点Ｏ作ON∥AC 交BC于点D， 过点Ｏ作OM∥BC，

∵

∴

∵

∴

∵

∴．

(3)关键：将沿点C所在的垂直于AB的直线翻折，折痕与AB的交点为H，使点C与点H重合，确定折痕MN，将沿点M所在的垂直于AB的直线翻折，折痕与AB的交点为E ，将沿点N所在的垂直于AB的直线翻折，折痕与AB的交点为F

证明思路：根据翻折的性质知：

,，MN是CH的垂直平分线，

∴,,

∴

∴

同理

∴，

∵

∴．