
【题目】已知:如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A、C的坐标分别为A(﹣3,0),C(1,0),![]() .
.
(1)求过点A、B的直线的函数表达式;
(2)在x轴上找一点D,连接DB,使得△ADB与△ABC相似(不包括全等),并求点D的坐标;
(3)在(2)的条件下,如P、Q分别是AB和AD上的动点,连接PQ,设AP=DQ=m,问是否存在这样的m使得以点A、P、Q为顶点的三角形与△ADB相似?如存在,请求出m的值;如不存在,请说明理由.

【答案】(1)直线AB的解析式为y=![]() x+
x+![]() ;(2)符合条件的D(
;(2)符合条件的D(![]() ,0);(3)符合要求的m的值为
,0);(3)符合要求的m的值为 ![]() 或
或![]() .
.
【解析】
(1)根据点A、B的坐标求出AC的长度再根据![]() 求出BC的长度 然后即可写出点B的坐标,设过点A,B的直线的函数表达式为y= kx+b,利用待定系数法求解即可得到直线AB的函数表达式;
求出BC的长度 然后即可写出点B的坐标,设过点A,B的直线的函数表达式为y= kx+b,利用待定系数法求解即可得到直线AB的函数表达式;
(2)过点B作BD⊥AB,交x轴于点D,D点为所求,继而求出D点坐标;
(3)在Rt△ABC中,由勾股定理得AB的值,当PQ// BD时,△APQ~△ABD ,解得m的值 ;当PQ⊥AD时,△APQ ~△ADB ,则解得m 的值.
(1)∵A(﹣3,0),C(1,0),
∴AC=4,
∵BC=![]() AC,
AC,
∴BC=![]() ×4=3,
×4=3,
∴B(1,3),
设直线AB的解析式为y=kx+b,
∴![]() ,
,
∴![]() ,
,
∴直线AB的解析式为y=![]() x+
x+![]() ;
;
(2)若△ADB与△ABC相似,
过点B作BD⊥AB交x轴于D,∴∠ABD=∠ACB=90°,如图1,
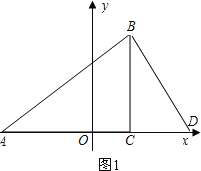
此时 ![]() =
=![]() ,即AB2=ACAD.
,即AB2=ACAD.
∵∠ACB=90°,AC=4,BC=3,
∴AB=5,
∴25=4AD,
∴AD=![]() ,
,
∴OD=AD﹣AO=![]() ﹣3=
﹣3=![]() ,
,
∴点D的坐标为( ![]() ,0).
,0).
即:符合条件的D( ![]() ,0).
,0).
(3)∵AP=DQ=m,
∴AQ=AD﹣QD=![]() ﹣m.
﹣m.
Ⅰ、若△APQ∽△ABD,如图2,
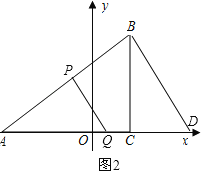
则有 ![]() =
=![]() ,
,
∴APAD=ABAQ,
∴![]() m=5(
m=5( ![]() ﹣m),
﹣m),
解得m=![]() ;
;
Ⅱ、若△APQ∽△ADB,如图3,
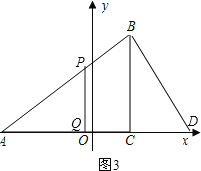
则有 ![]() =
=![]() ,
,
∴APAB=ADAQ,
∴5m=![]() (
( ![]() ﹣m),
﹣m),
解得:m=![]() ,
,
综上所述:符合要求的m的值为 ![]() 或
或 ![]() .
.


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
【题目】如图1,将一块含有![]() 角的三角板放置在一条直线上,
角的三角板放置在一条直线上,![]() 边与直线
边与直线![]() 重合,
重合,![]() 边的垂直平分线与边
边的垂直平分线与边![]() 分别交于
分别交于![]() 两点,连接
两点,连接![]() .
.


(1) ![]() 是 三角形;
是 三角形;
(2)直线![]() 上有一动点
上有一动点![]() (不与点
(不与点![]() 重合) ,连接
重合) ,连接![]() 并把
并把![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 到
到![]() ,连接
,连接![]() .当点
.当点![]() 在图2所示的位置时,证明
在图2所示的位置时,证明![]() .我们可以用
.我们可以用![]() 来证明
来证明![]() ,从而得到
,从而得到![]() .当点
.当点![]() 移动到图3所示的位置时,结论是否依然成立?若成立,请你写出证明过程;若不成立,请你说明理由.
移动到图3所示的位置时,结论是否依然成立?若成立,请你写出证明过程;若不成立,请你说明理由.
(3)当点![]() 在
在![]() 边上移动时(不与点
边上移动时(不与点![]() 重合),
重合),![]() 周长的最小值是 .
周长的最小值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李先生参加了清华同方电脑公司推出的分期付款购买电脑活动,他购买的电脑价格为![]() 万元,交了首付之后每月付款
万元,交了首付之后每月付款![]() 元,
元,![]() 月结清余款.
月结清余款.![]() 与
与![]() 的函数关系如图所示,试根据图象提供的信息回答下列问题.
的函数关系如图所示,试根据图象提供的信息回答下列问题.

![]() 确定
确定![]() 与
与![]() 的函数关系式,并求出首付款的数目;
的函数关系式,并求出首付款的数目;
![]() 如打算每月付款不超过
如打算每月付款不超过![]() 元,李先生至少几个月才能结清余款?
元,李先生至少几个月才能结清余款?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料:
问题:如图,在正方形![]() 和平行四边形
和平行四边形![]() 中,点
中,点![]() ,
,![]() ,
,![]() 在同一条直线上,
在同一条直线上,![]() 是线段
是线段![]() 的中点,连接
的中点,连接![]() ,
,![]() .
.
探究:当![]() 与
与![]() 的夹角为多少度时,平行四边形
的夹角为多少度时,平行四边形![]() 是正方形?
是正方形?
小聪同学的思路是:首先可以说明四边形![]() 是矩形;然后延长
是矩形;然后延长![]() 交
交![]() 于点
于点![]() ,构造全等三角形,经过推理可以探索出问题的答案.
,构造全等三角形,经过推理可以探索出问题的答案.
请你参考小聪同学的思路,探究并解决这个问题.

(1)求证:四边形![]() 是矩形;
是矩形;
(2)![]() 与
与![]() 的夹角为________度时,四边形
的夹角为________度时,四边形![]() 是正方形.
是正方形.
理由:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为美化校园,计划对面积为1800m2的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为400 m2区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积分别是多少m2?
(2)若学校每天需付给甲队的绿化费用是0.4万元,乙队为0.25万元,要使这次的绿化总费用不超过8万元,至少应安排甲队工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则OF的长度是( )

A. 3cm B. ![]() cm C. 2.5cm D.
cm C. 2.5cm D. ![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(5,3),B(6,5),C(4,6).
(1)画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标.
(2)将△A1B1C1向左平移6个单位,再向上平移5个单位,画出平移后得到的△A2B2C2,并写出点B2的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com