
【题目】八年级甲班和乙班各推选10名同学进行投篮比赛,按照比赛规则,每人各投了10个球;将两班选手的进球数绘制成如下尚不完整的统计图表:
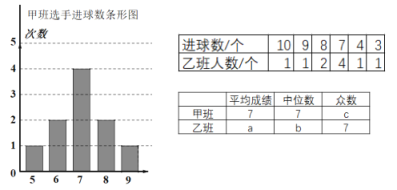
(1)表格中b=_________.c=_________;并求a的值;
(2)如果要从这两个班中选出一个班代表年级参加学校的投篮比赛,争取夺得总进球数团体第一名,你认为应该选择哪个班?如果要争取个人进球数进入学校前三名,你认为应该选择哪个班?请说明理由。
【答案】(1)7,7,7;(2)选择甲班;选择乙班.
【解析】
(1)利用平均数、中位数和众数的定义直接求出;
(2)根据方差和个人发挥的最好成绩进行选择.
(1)甲班选手进球数次数最多的是7个球,共有4次,故众数为7;
乙班选手进球数的平均数为![]()
按大小顺序排列,最中间的两个数为:7,7,故其中位数为:![]() ;
;
∴a=7,b=7,c=7;
(2)甲班S12=![]() [(5-7)2+(6-7)2×2+2×(8-7)2+4×(7-7)2+1×(9-7)2]=1.2,
[(5-7)2+(6-7)2×2+2×(8-7)2+4×(7-7)2+1×(9-7)2]=1.2,
乙班S22=![]() [(10-7)2+(9-7)2+2×(8-7)2+4×(7-7)2+(4-7)2+(3-7)2]=4.
[(10-7)2+(9-7)2+2×(8-7)2+4×(7-7)2+(4-7)2+(3-7)2]=4.
∵乙方差>甲方差,
∴要争取夺取总进球团体第一名,应选甲班.
∵乙班有一位百发百中的出色选手,
∴要进入学校个人前3名,应选乙班.


 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案科目:初中数学 来源: 题型:
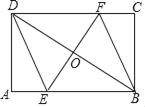
【题目】如图,在矩形ABCD中,AB=8,BC=4,过对角线BD的中点O的直线分别交AB、CD于点E、F,连接DE,BF.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校组织的“学习强国”知识竞赛中,每班参加比赛的人数相同,成绩分为![]() ,
,![]() ,
,![]() ,
,![]() 四个等级其中相应等级的得分依次记为
四个等级其中相应等级的得分依次记为![]() 分,
分,![]() 分,
分,![]() 分和
分和![]() 分.年级组长张老师将
分.年级组长张老师将![]() 班和
班和![]() 班的成绩进行整理并绘制成如下的统计图:
班的成绩进行整理并绘制成如下的统计图:
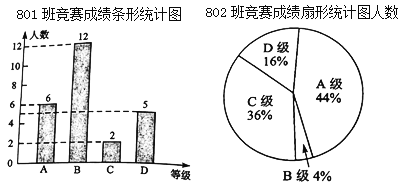
(1)在本次竞赛中,![]() 班
班![]() 级的人数有多少。
级的人数有多少。
(2)请你将下面的表格补充完整:
成绩 班级 | 平均数(分) | 中位数 (分) | 众数 (分) | B级及以上人数 |
|
|
|
| |
|
|
|
(3)结合以上统计量,请你从不同角度对这次竞赛成绩的结果进行分析(写出两条)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有20筐白菜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
![]()
(1)20筐白菜中,最重的一筐比最轻的一筐多重多少千克?
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价2.8元,则出售这20筐白菜可卖多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(规律探索)如图所示的是由相同的小正方形组成的图形,每个图形的小正方形个数为Sn,n是正整数.观察下列图形与等式之间的关系.
第一组:
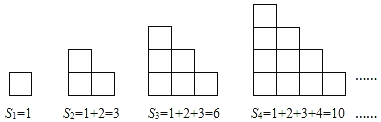
第二组:
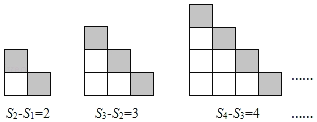
第三组:
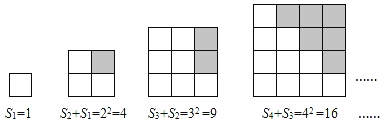
(规律归纳)
(1)S7﹣S6= ;Sn﹣Sn﹣1= .
(2)S7+S6= ;Sn+Sn﹣1= .
(规律应用)
(3)计算![]() 的结果为 .
的结果为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若关于x的一元二次方程ax2+bx+c=0(a≠0)的两个实数根为x1,x2(x1<x2),分别以x1,x2为横坐标和纵坐标得到点M(x1,x2),则称点M为该一元二次方程的衍生点.
(1)若方程为x2-2x=0,写出该方程的衍生点M的坐标.
(2)若关于x的一元二次方程x2-(2m+1)x+2m=0(m<0)的衍生点为M,过点M向x轴和y轴作垂线,两条垂线与坐标轴恰好围成一个正方形,求m的值.
(3)是否存在b,c,使得不论k(k≠0)为何值,关于x的方程x2+bx+c=0的衍生点M始终在直线y=kx-2(k-2)的图象上,若有请直接写出b,c的值,若没有说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个矩形娱乐场所,其设计方案如图所示.其中半圆形休息区和矩形游泳池以外的地方都是绿地.试解答下列问题:
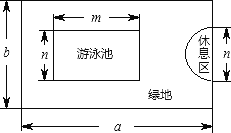
(1)游泳池和休息区的面积各是多少?
(2)绿地面积是多少?
(3)如果这个娱乐场所的长是宽的1.5倍,要求绿地面积占整个面积的一半以上.小亮同学根据要求,设计的游泳池的长和宽分别是大矩形长和宽的一半,你说他的设计符合要求吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(3,m),B(﹣2,﹣3)是直线AB和某反比例函数的图象的两个交点.
(1)求直线AB和反比例函数的解析式;
(2)观察图象,直接写出当x满足什么范围时,直线AB在双曲线的下方;
(3)反比例函数的图象上是否存在点C,使得△OBC的面积等于△OAB的面积?如果不存在,说明理由;如果存在,求出满足条件的所有点C的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司购进某种矿石原料300吨,用于生产甲、乙两种产品,生产1吨甲产品或1吨乙产品所需该矿石和煤原料的吨数如下表:
产品资源 | 甲 | 乙 |
矿石(吨) | 10 | 4 |
煤(吨) | 4 | 8 |
生产1吨甲产品所需成本费用为4000元,每吨售价4600元;
生产1吨乙产品所需成本费用为4500元,每吨售价5500元,
现将该矿石原料全部用完,设生产甲产品x吨,乙产品m吨,公司获得的总利润为y元.
(1)写出m与x之间的关系式
(2)写出y与x之间的函数表达式,并写出自变量的范围
(3)若用煤不超过200吨,生产甲产品多少吨时,公司获得的总利润最大,最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com