Question

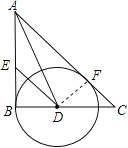
【题目】如图，在Rt△ABC中，∠B=90°，∠A的平分线交BC于D，E为AB上一点，DE=DC，以D为圆心，以DB的长为半径画圆．

求证：（1）AC是⊙D的切线；（2）AB+EB=AC．

Answer 1

【答案】（1）证明见试题解析；（2）证明见试题解析．

【解析】试题（1）过点D作DF⊥AC于F，求出BD=DF等于半径，得出AC是⊙D的切线．

（2）先证明△BDE≌△FCD（HL），根据全等三角形对应边相等及切线的性质的AB=AF，得出AB+EB=AC．

证明：（1）过点D作DF⊥AC于F；（1分）

∵AB为⊙D的切线，AD平分∠BAC，

∴BD=DF，（3分）

∴AC为⊙D的切线．（4分）

（2）∵AC为⊙D的切线，

∴∠DFC=∠B=90°，

在Rt△BDE和Rt△FCD中；

∵BD=DF，DE=DC，

∴Rt△BDE≌Rt△FCD（HL），（6分）

∴EB=FC．（8分）

∵AB=AF，

∴AB+EB=AF+FC，

即AB+EB=AC．（10分）