
【题目】如图,ABCD的对角线AC、BD相交于点M,点M在以AB为直径的⊙O上,AD与⊙O相交于点E,连接ME.
(1)求证:ME=MD;
(2)当∠DAB=30°时,判断直线CD与⊙O的位置关系,并说明理由.
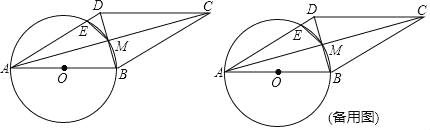
【答案】(1)证明见解析;(2)直线CD与⊙O相切.
【解析】
(1)由圆周角定理可得∠AMB=90°,可证ABCD是菱形,可得AD=AB,根据等腰三角形的性质和圆内接四边形的性质可得∠ADB=∠DEM,即MEI=DM;
(2)过O作OH⊥CD于H,过D作DF⊥AB于F,由题意可证四边形OFDH是平行四边形,可得OH=DF,根据菱形的性质和直角三角形的性质可得OH=![]() AB,根据切线的判定,可证直线CD与⊙O相切.
AB,根据切线的判定,可证直线CD与⊙O相切.
证明:(1)∵AB是⊙O直径,
∴∠AMB=90°,
∴ABCD是菱形,
∴AD=AB,
∴∠ADB=∠ABD,
∵四边形AEMB是圆内接四边形,
∴∠DEM=∠ABD,
∴∠ADB=∠DEM,
∴ME=MD.
(2)直线CD与⊙O相切
理由如下:
过O作OH⊥CD于H,过D作DF⊥AB于F,
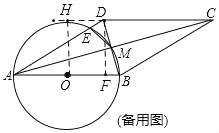
∵DF⊥AB,AB∥CD,
∴DF⊥CD,且OH⊥CD,
∴OH∥DF,且AB∥CD,
∴四边形OFDH是平行四边形,
∴OH=DF,
∵在Rt△ADF中,∠DAF=30°,
∴DF=![]() AD,
AD,
又∵四边形ABCD是菱形,
∴AD=AB,
∴OH=DF=![]() AD=
AD=![]() AB,
AB,
又∵OH⊥CD,
∴直线CD与⊙O相切.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】“十九大”报告提出了我国将加大治理环境污染的力度,还我青山绿水,其中雾霾天气让环保和健康问题成为焦点,为了调查学生对雾霾天气知识的了解程度,某校在全校学生中抽取400名同学做了一次调查,根据调查统计结果,绘制了不完整的一种统计图表.
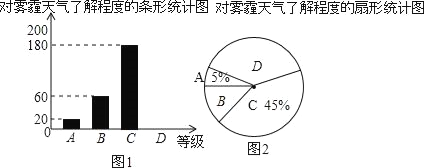
对雾霾了解程度的统计表
对雾霾的了解程度 | 百分比 |
A.非常了解 | 5% |
B.比较了解 | m |
C.基本了解 | 45% |
D.不了解 | n |
请结合统计图表,回答下列问题:
(1)统计表中:m= ,n= ;
(2)请在图1中补全条形统计图;
(3)请问在图2所示的扇形统计图中,D部分扇形所对应的圆心角是多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去学校食堂就餐,经常会在一个买菜窗口前等待,经调查发现,同学的舒适度指数y与等时间x(分)之间满足反比例函数关系,如下表:
等待时间x | 1 | 2 | 5 | 10 | 20 |
舒适度指数y | 100 | 50 | 20 | 10 | 5 |
已知学生等待时间不超过30分钟
(1)求y与x的函数关系式,并写出自变量x的取值范围.
(2)若等待时间8分钟时,求舒适度的值;
(3)舒适度指数不低于10时,同学才会感到舒适.请说明,作为食堂的管理员,让每个在窗口买菜的同学最多等待多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是⊙O的内接四边形,AC为直径,点B是弧AC的中点,若AC=7,BD=6,则由四个弓形组成的阴影部分的面积为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
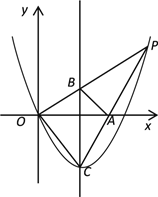
【题目】如图,已知抛物线y=ax2+bx的顶点为C(1,![]() ),P是抛物线上位于第一象限内的一点,直线OP交该抛物线对称轴于点B,直线CP交x轴于点A.
),P是抛物线上位于第一象限内的一点,直线OP交该抛物线对称轴于点B,直线CP交x轴于点A.
(1)求该抛物线的表达式;
(2)如果点P的横坐标为m,试用m的代数式表示线段BC的长;
(3)如果△ABP的面积等于△ABC的面积,求点P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB是⊙O的直径,点P在BA的延长线上,弦CD交AB于E,连接OD、PC、BC,∠AOD=2∠ABC,∠P=∠D,过E作弦GF⊥BC交圆与G、F两点,连接CF、BG.则下列结论:①CD⊥AB;②PC是⊙O的切线;③OD∥GF;④弦CF的弦心距等于![]() BG.则其中正确的是( )
BG.则其中正确的是( )
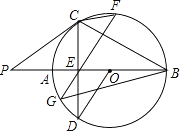
A. ①②④ B. ③④ C. ①②③ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
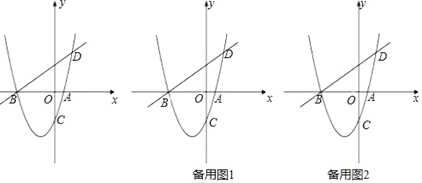
【题目】(12分)如图,已知抛物线y=ax2+bx﹣2(a≠0)与x轴交于A、B两点,与y轴交于C点,直线BD交抛物线于点D,并且D(2,3),B(﹣4,0).
(1)求抛物线的解析式;
(2)已知点M为抛物线上一动点,且在第三象限,顺次连接点B、M、C,求△BMC面积的最大值;
(3)在(2)中△BMC面积最大的条件下,过点M作直线平行于y轴,在这条直线上是否存在一个以Q点为圆心,OQ为半径且与直线AC相切的圆?若存在,求出圆心Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
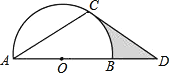
【题目】如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com