
【题目】把△ABC经过平移后得到△A′B′C′,已知A(4,3),B(3,1),B′(1,﹣1),C′(2,0),则△ABC的面积为( )
A.![]()
B.![]()
C.1
D.2
【答案】B
【解析】∵把△ABC经过平移后得到△A′B′C′,B(3,1)的对应点是B′(1,﹣1),
∴B点向左平移2个单位,再向下平移2个单位,
∵A(4,3)的对应点A′的坐标是(4﹣2,3﹣2),即A′(2,1),
C′(2,0))的对应点C的坐标是(2+2,0+2),即(4,2),
过B作BD⊥AC于D,
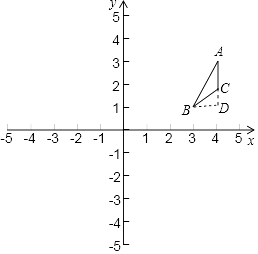
∵A(4,3),C(4,2),
∴AC⊥X轴,
∴AC=3﹣2=1,BD=4﹣3=1,
∴△ABC的面积是 ![]() AC×BD=
AC×BD= ![]() ×1×1=
×1×1= ![]() .
.
所以答案是:B.
![]()
【考点精析】解答此题的关键在于理解坐标与图形变化-平移的相关知识,掌握新图形的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点;连接各组对应点的线段平行且相等.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,下图是汽车行驶速度(千米/时)和时间(分)的关系图,下列说法其中正确的个数为( )
( 1 )汽车行驶时间为40分钟;
( 2 )AB表示汽车匀速行驶;
( 3 )在第30分钟时,汽车的速度是90千米/时;
( 4 )第40分钟时,汽车停下来了.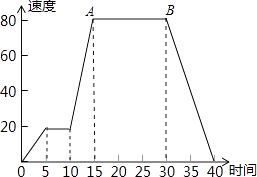
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
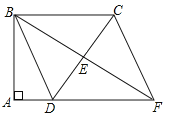
【题目】如图,四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.
(1)求证:四边形BDFC是平行四边形;
(2)若△BCD是等腰三角形,求四边形BDFC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在等边△ABC的边AC的延长线上取一点E,以CE为边作等边△CDE,使它与△ABC位于直线AE的同侧. 
(1)同学们对图1进行了热烈的讨论,猜想出如下结论,你认为正确的有(填序号). ①△ACD≌△BCE;②△ACP≌△BCQ; ③△DCP≌△ECQ;④∠ARB=60°;⑤△CPQ是等边三角形.
(2)当等边△CED绕C点旋转一定角度后(如图2),(1)中有哪些结论还是成立的?并对正确的结论分别予以证明. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店为了促销一种定价为3元的商品,采取下列方式优惠销售:若一次性购买不超过5件,按原价付款;若一次性购买5件以上,超过部分按原价八折付款.如果小明有30元钱,那么他最多可以购买该商品( )
A. 9件 B. 10件 C. 11件 D. 12件
查看答案和解析>>
科目:初中数学 来源: 题型:
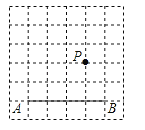
【题目】如图,在方格纸中,点A,B,P都在格点上.请按要求画出以AB为边的格点四边形,使P在四边形内部(不包括边界上),且P到四边形的两个顶点的距离相等.
(1)在图甲中画出一个ABCD.
(2)在图乙中画出一个四边形ABCD,使∠D=90°,且∠A≠90°.(注:图甲、乙在答题纸上)
查看答案和解析>>
科目:初中数学 来源: 题型:
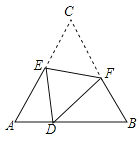
【题目】如图,D是等边△ABC边AB上的一点,且AD:DB=1:2,现将△ABC折叠,使点C与D重合,折痕为EF,点E,F分别在AC和BC上,则CE:CF=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com