
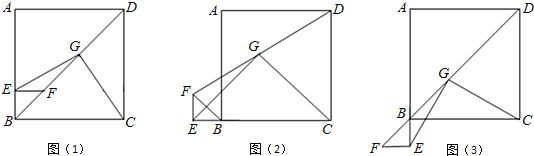
【题目】在正方形ABCD的边AB上任取一点E,作EF⊥AB交BD于点F,取FD的中点G,连结EG、CG.
(1)如图1,求证EG=CG且EG⊥CG.
(2)如图2将△BEF绕点B逆时针旋转90度,求线段EG和CG有怎么样的关系,并证明你的结论.
(3)如图3,将△BEF绕点B逆时针旋转180度,线段EG和CG有怎么样的关系?写出你的猜想,不需证明.
【答案】(1)EG=CG,且EG⊥CG.证明见解析;(2)证明见解析;(3)EG=CG且EG⊥CG.
【解析】(1)过点G作GH⊥BD于G交CD于H,通过条件证明△HGE≌△ICG,就可以得出结论EG=CG,EG⊥CG;
(2)作GH⊥BC于H,根据平行线等分线段定理就可以得出EH=CH,再根据中垂线的性质就可以得出EG=EC,过点G作GP⊥BD于G交CB于P,最后通过证明三角形全等就可以得出结论EG⊥CG;
(3)延长FE交DC延长线于M,连MG.可证四边形BEMC是矩形,得到BE=CM,∠EMC=90°.再证△BEF为等腰直角三角形,得到BE=EF,∠F=45°,EF=CM.
由直角三角形斜边上的中线等于斜边的一半得到MG=![]() FD=FG.通过证明
FD=FG.通过证明
FM=DM和∠F=∠GMC.得到△GFE≌△GMC,即可得到结论.
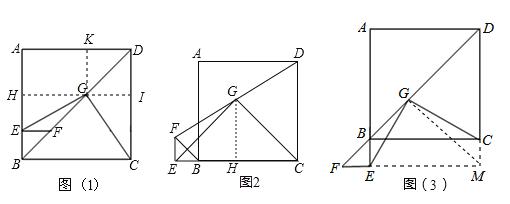
(1)过GH⊥AB于点H,延长HG交CD于点I,作GK⊥AD于点K.
则四边形GIDK是正方形,四边形AKGH是矩形,∴AK=HG,KD=DI=GI=AH.
∵AD=CD,∴IC=HG.
∵AD∥GH∥EF,G是DF的中点,∴HA=HE,∴HE=GI.
在Rt△HGE和Rt△ICG中,∵ ,∴Rt△HGE≌Rt△ICG(SAS),∴EG=CG,∠HGE=∠GCI,∠HEG=∠CGI,∴∠HGE+∠CGI=90°,∴∠EGC=90°,∴EG⊥CG;
,∴Rt△HGE≌Rt△ICG(SAS),∴EG=CG,∠HGE=∠GCI,∠HEG=∠CGI,∴∠HGE+∠CGI=90°,∴∠EGC=90°,∴EG⊥CG;
(2)EG=CG,且EG⊥CG. 证明如下:
图2中,作GH⊥BC,则EF∥GH∥CD.
又∵G是DF的中点,∴EH=CH,则GH是BC的中垂线,∴GE=CG.
∵EF=EB,BC=CD
∴EF+CD=EC.
∵G是DF的中点,EH=CH,则GH=![]() (EF+CD),∴GH=
(EF+CD),∴GH=![]() EC,∴△EGC是等腰直角三角形,∴EG=CG,且EG⊥CG;
EC,∴△EGC是等腰直角三角形,∴EG=CG,且EG⊥CG;
(3)结论:EG=CG,且EG⊥CG.理由如下:
延长FE交DC延长线于M,连MG.
∵∠AEM=90°,∠EBC=90°,∠BCM=90°,∴四边形BEMC是矩形,∴BE=CM,∠EMC=90°.
∵BD平分∠ABC,∠ABC=90°,∴∠EBF=45°.
又∵EF⊥AB,∴△BEF为等腰直角三角形,
∴BE=EF,∠F=45°,∴EF=CM.
∵∠EMC=90°,FG=DG,
∴MG=![]() FD=FG.
FD=FG.
∵BC=EM,BC=CD,∴EM=CD.
∵EF=CM,∴EF+EM=CM+DC,即FM=DM.
又∵FG=DG,∠CMG=![]() ∠EMC=45°,∴∠F=∠GMC.
∠EMC=45°,∴∠F=∠GMC.
在△GFE和△GMC中,∵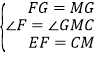 ,∴△GFE≌△GMC(SAS),∴EG=CG,∠FGE=∠MGC.
,∴△GFE≌△GMC(SAS),∴EG=CG,∠FGE=∠MGC.
∵∠FMC=90°,MF=MD,FG=DG,∴MG⊥FD,∴∠FGE+∠EGM=90°,∴∠MGC+∠EGM=90°,即∠EGC=90°,∴EG⊥CG.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,将直角三角形ABC沿着斜边AC的方向平移到△DEF的位置(A、D. C. F四点在同一条直线上).直角边DE交BC于点G.如果BG=4,EF=12,△BEG的面积等于4,那么梯形ABGD的面积是( )

A.16B.20C.24D.28
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有A,B,C,D四个整数点(即各点均表示整数),且2AB=BC=3CD,若A,D两点表示的数分别为-5和6,点E为BD的中点,在数轴上的整数点中,离点E最近的点表示的数是( )
![]()
A.2B.1
C.0D.-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A=2x2﹣6ax+3,B=﹣7x2﹣8x﹣1,按要求完成下列各小题.
(1)若A+B的结果中不存在含x的一次项,求a的值;
(2)当a=﹣2时,求A﹣3B的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料阅读
角是一种基本的几何图像,如图1角可以看作由一条射线绕着它的端点旋转而形成的图形.钟面上的时针与分针给我们以角的形象.如果把图2作为钟表的起始状态,对于一个任意时刻时针与分针的夹角度数可以用下面的方法确定.

因为时针绕钟面转一圈(![]() )需要12小时,所以时针每小时转过
)需要12小时,所以时针每小时转过![]() .
.
如图3中![]() 时针就转过
时针就转过![]() .
.
因为分针绕钟面转一圈(![]() )需要60分钟,所以分针每分钟转过
)需要60分钟,所以分针每分钟转过![]() .
.
如图4中![]() 分针就转过
分针就转过![]() .
.
再如图5中![]() 时针转过的度数为
时针转过的度数为![]() ,分针转过的度数记为
,分针转过的度数记为![]() ,此时,分针转过的度数大于时针转过的度数,所以
,此时,分针转过的度数大于时针转过的度数,所以![]() 时针与分针的夹角为
时针与分针的夹角为![]() .
.
知识应用
请使用上述方法,求出![]() 时针与分针的夹角.
时针与分针的夹角.
拓广探索
张老师某周六上午7点多去菜市场买菜,走时发现家中钟表时钟与分针的夹角是直角,买菜回到家发现钟表时针与分针的夹角还是直角,可以确定的是张老师家的钟表没有故障,走时正常,且回家时间还没到上午8点,请利用上述材料所建立数学模型列方程,求出张老师约7点多少分出门买菜?约7点多少分回到家?(结果用四舍五入法精确到分.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场今年![]() 月的商品销售总额一共是
月的商品销售总额一共是![]() 万元,如图(1)表示的是其中每个月销售总额的情况,图(2)表示的是商场服装部各月销售额占商场当月销售总额的百分比情况,观察图(1)、图(2),下列说法不正确的是( )
万元,如图(1)表示的是其中每个月销售总额的情况,图(2)表示的是商场服装部各月销售额占商场当月销售总额的百分比情况,观察图(1)、图(2),下列说法不正确的是( )
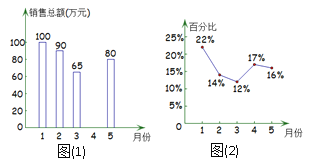
A. 4月份商场的商品销售总额是75万元 B. 1月份商场服装部的销售额是22万元
C. 5月份商场服装部的销售额比4月份减少了 D. 3月份商场服装部的销售额比2月份减少了
查看答案和解析>>
科目:初中数学 来源: 题型:
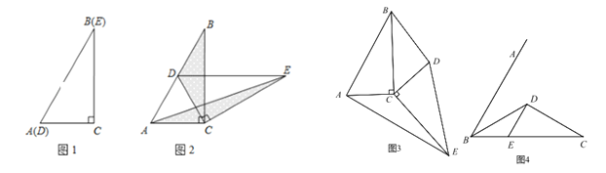
【题目】如图 1,两个完全相同的三角形纸片 ABC 和 DEC 重合放置,其中∠C=90°,∠B=∠E=30°.
⑴ 操作发现:如图 2,固定△ABC,使△DEC 绕点 C 旋转,当点 D 恰好落在 AB 边上时, 填空:
①线段 DE 与 AC 的位置关系是 ;
②设△BDC 的面积为 S1,△AEC 的面积为 S2,则 S1 与 S2 的数量关系是 .
⑵ 猜想论证
当△DEC 绕点 C 旋转到如图 3 所示的位置时,请猜想(1)中 S1 与 S2 的数量关系是否仍 然成立?若成立,请证明;若不成立,请说明理由.
⑶ 拓展探究
已知∠ABC=60°,BD 平分∠ABC,BD=CD,BE=6,DE∥AB 交 BC 于点 E(如图 4).若在射线 BA 上存在点 F,使 S△DCF=S△BDE,请求相应的 BF 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
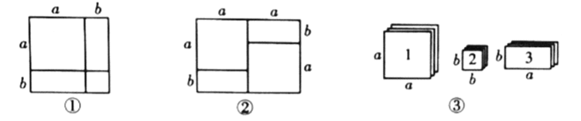
某些代数恒等式可用一些卡片拼成的图形的面积来解释.例如,图①可以解释![]() ,因此,我们可以利用这种方法对某些多项式进行因式分解.
,因此,我们可以利用这种方法对某些多项式进行因式分解.
根据阅读材料回答下列问题:
(1)如图②所表示的因式分解的恒等式是________________________.
(2)现有足够多的正方形和长方形卡片(如图③),试画出一个用若干张1号卡片、2号卡片和3号卡片拼成的长方形(每两张卡片之间既不重叠,也无空隙),使该长方形的面积为![]() ,并利用你画的长方形的面积对
,并利用你画的长方形的面积对![]() 进行因式分解.
进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
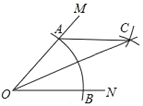
【题目】如图,在∠MON中,以点O为圆心,任意长为半径作弧,交射线OM于点A,交射线ON于点B,再分别以A、B为圆心,OA的长为半径作弧,两弧在∠MON的内部交于点C,作射线OC,若OA=5,AB=6,则点B到AC的距离为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com