
分析 (1)根据根的判别式,可得不等式,根据解不等式,可得答案;
(2)根据根与系数的关系,可得关于m的方程,根据解方程,可得答案.
解答 解:(1)由关于x的方程x2-(m+3)x+$\frac{{m}^{2}+2}{4}$=0,得
△=b2-4ac=[-(m+3)]2-4×1×$\frac{{m}^{2}+2}{4}$≥0,
解得m≥-$\frac{7}{6}$;
(2)由根于系数的关系,得x1+x2=m+3,x1x2=$\frac{{m}^{2}+2}{4}$>0,
x12+x22=|x1x2|+$\frac{41}{2}$,
(x1+x2)2=3x1x2+$\frac{41}{2}$,
(m+3)2=$\frac{3({m}^{2}+2)}{4}$+$\frac{41}{2}$,
解得m1=-26(不符合题意,舍),m2=2.
点评 本题考查了根与系数的关系,利用根与系数的关系得出关于m的方程是解题关键.


科目:初中数学 来源: 题型:填空题
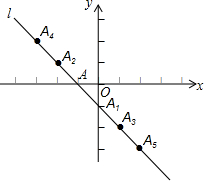 如图在平面直角坐标系xOy中,直线l经过点 A(-1,0),点 A1,A2,A3,A4,A5,…按所示的规律排列在直线l上.若直线l上任意相邻两个点的横坐标都相差1、纵坐标也都相差1,若点An(n为正整数)的横坐标为2015,则n=4031.
如图在平面直角坐标系xOy中,直线l经过点 A(-1,0),点 A1,A2,A3,A4,A5,…按所示的规律排列在直线l上.若直线l上任意相邻两个点的横坐标都相差1、纵坐标也都相差1,若点An(n为正整数)的横坐标为2015,则n=4031.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
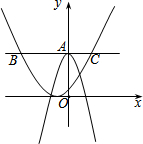 如图,在平面直角坐标系中,过点A与x轴平行的直线交抛物线y=$\frac{1}{3}{(x+1)^2}$于点B、C,线段BC的长度为6,抛物线y=-2x2+b与y轴交于点A,则b=( )
如图,在平面直角坐标系中,过点A与x轴平行的直线交抛物线y=$\frac{1}{3}{(x+1)^2}$于点B、C,线段BC的长度为6,抛物线y=-2x2+b与y轴交于点A,则b=( )| A. | 1 | B. | 4.5 | C. | 3 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
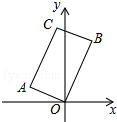 如图,在矩形AOBC中,点A的坐标(-2,1),点C的纵坐标是4,则B、C两点的坐标分别是( )
如图,在矩形AOBC中,点A的坐标(-2,1),点C的纵坐标是4,则B、C两点的坐标分别是( )| A. | ($\frac{7}{4}$,$\frac{7}{2}$)、(-$\frac{1}{2}$,4) | B. | ($\frac{3}{2}$,3)、(-$\frac{2}{3}$,4) | C. | ($\frac{3}{2}$,3)、(-$\frac{1}{2}$,4) | D. | ($\frac{7}{4}$,$\frac{7}{2}$)、(-$\frac{2}{3}$,4) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 次数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 人数 | 1 | 8 | 10 | 7 | 6 | 6 | 6 | 4 | 1 | 2 | 0 |
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6.2×1010元 | B. | 6.2×1011元 | C. | 6.2×1012元 | D. | 0.62×1012元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com