
在矩形ABCD中, ,点G,H分别在边AB,DC上,且HA=HG,点E为AB边上的一个动点,连接HE,把△AHE沿直线HE翻折得到△FHE.
,点G,H分别在边AB,DC上,且HA=HG,点E为AB边上的一个动点,连接HE,把△AHE沿直线HE翻折得到△FHE.
(1)如图1,当DH=DA时,
①填空:∠HGA= 度;
②若EF∥HG,求∠AHE的度数,并求此时a的最小值;
(2)如图3,∠AEH=60°,EG=2BG,连接FG,交边FG,交边DC于点P,且FG⊥AB,G为垂足,求a的值.

(1)①45;②当∠AHE为锐角时,∠AHE=22.5°时,a的最小值是2;当∠AHE为钝角时,∠AHE=112.5°时,a的最小值是 ;(2)
;(2) .
.
【解析】
试题分析:(1)①根据矩形的性质和已知条件得出∠HAE=45°,再根据HA=HG,得出∠HAE=∠HGA,从而得出答案解决:
∵四边形ABCD是矩形,∴∠ADH=90°.
∵DH=DA,∴∠DAH=∠DHA=45°.∴∠HAE=45°.
∵HA=HG,∴∠HAE=∠HGA=45°
②分∠AHE为锐角和钝角两种情况讨论即可.
(2)过点H作HQ⊥AB于Q,根据矩形的性质得出∠D=∠DAQ=∠AQH=90°,得出四边形DAQH为矩形,设AD=x,GB=y,则HQ=x,EG=2y,由折叠的性质可知∠AEH=∠FEH=60°,得出∠FEG=60°,在Rt△EFG中,根据特殊角的三角函数值求出EG和EQ的值,再由折叠的性质得出AE=EF,求出y关于x的表达式,从而求出AB=2AQ+GB,即可根据比值消去参数x得出a的值.
试题解析:【解析】
(1)①45.
②分两种情况讨论:
第一种情况:如答图1,∠AHE为锐角时,
∵∠HAG=∠HGA=45°,∴∠AHG=90°.
由折叠可知:∠HAE=∠F=45°,∠AHE=∠FHE,
∵EF∥HG,∴∠FHG=∠F=45°.
∴∠AHF=∠AHG ∠FHG=45°,即∠AHE+∠FHE=45°.
∠FHG=45°,即∠AHE+∠FHE=45°.
∴∠AHE=22.5°.
此时,当B与G重合时,a的值最小,最小值是2.

第二种情况:如答图2,∠AHE为钝角时,
∵EF∥HG,∴∠HGA=∠FEA=45°,即∠AEH+∠FEH=45°.
由折叠可知:∠AEH=∠FEH,∴∠AEH=∠FEH=22.5°.
∵EF∥HG,∴∠GHE=∠FEH=22.5°.
∴∠AHE=90°+22.5°=112.5°.
此时,当B与E重合时,a的值最小,
设DH=DA=x,则AH=CH=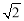 x,
x,
在Rt△AHG中,∠AHG=90°,由勾股定理得:AG=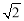 AH=2x,
AH=2x,
∵∠AEH=∠FEH,∠GHE=∠FEH,∴∠AEH=∠GHE.∴GH=GE=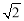 x.
x.
∴AB=AE=2x+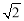 x.
x.
∴a的最小值是 .
.
综上所述,当∠AHE为锐角时,∠AHE=22.5°时,a的最小值是2;当∠AHE为钝角时,∠AHE=112.5°时,a的最小值是 .
.

(2)如答图3:过点H作HQ⊥AB于Q,则∠AQH=∠GOH=90°,
在矩形ABCD中,∠D=∠DAQ=90°,
∴∠D=∠DAQ=∠AQH=90°.
∴四边形DAQH为矩形.∴AD=HQ.
设AD=x,GB=y,则HQ=x,EG=2y,
由折叠可知:∠AEH=∠FEH=60°,∴∠FEG=60°.
在Rt△EFG中,EG=EF×cos60°=4y× ,
,
在Rt△HQE中, ,
,
∴ .
.
∵HA=HG,HQ⊥AB,∴AQ=GQ= .
.
∴AE=AQ+QE=  .
.
由折叠可知:AE=EF,即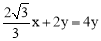 ,即
,即 .
.
∴AB=2AQ+GB= .
.
∴ .
.

考点:1.四边形综合题;2.单动点和折叠问题;3.矩形的判定和性质;4.等腰直角三角形的判定和性质;5.折叠对称的性质;6.勾股定理;7. 锐角三角函数定义;8.特殊角的三角函数值;9.分类思想和消参的待定系数法应用.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源:2014年初中毕业升学考试(湖南娄底卷)数学(解析版) 题型:选择题
函数 y= 中自变量x的取值范围为( )
中自变量x的取值范围为( )
A.x≥0 B.x≥﹣2 C.x≥2 D.x≤﹣2
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖北武汉卷)数学(解析版) 题型:选择题
在一次中学生田径运动会上,参加调高的15名运动员的成绩如下表所示:
成绩(m) | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
人数 | 1 | 2 | 4 | 3 | 3 | 2 |
那么这些运动员跳高成绩的众数是( )
A.4 B.1.75 C.1.70 D.1.65
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖北宜昌卷)数学(解析版) 题型:解答题
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB.
(1)求∠CAD的度数;
(2)延长AC至E,使CE=AC,求证:DA=DE.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖北宜昌卷)数学(解析版) 题型:选择题
要使分式 有意义,则的取值范围是( )
有意义,则的取值范围是( )
A. x≠1 B. x>1 C. x<1 D. x≠﹣1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com