
【题目】如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(8,8),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG.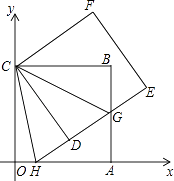
(1)求证:△CBG≌△CDG;
(2)求∠HCG的度数;判断线段HG、OH、BG的数量关系,并说明理由;
(3)连结BD、DA、AE、EB得到四边形AEBD,在旋转过程中,四边形AEBD能否为矩形?如果能,请求出点H的坐标;如果不能,请说明理由.
【答案】
(1)∵正方形ABCO绕点C旋转得到正方形CDEF,
∴CD=CB,∠CDG=∠CBG=90°.
在Rt△CDG和Rt△CBG中,
![]() ,
,
∴△CDG≌△CBG(HL)
(2)解:∵△CDG≌△CBG,
∴∠DCG=∠BCG,DG=BG.
在Rt△CHO和Rt△CHD中,
∵ ![]() ,
,
∴△CHO≌△CHD(HL),
∴∠OCH=∠DCH,OH=DH,
∴∠HCG=∠HCD+∠GCD= ![]() ∠OCD+
∠OCD+ ![]() ∠DCB=
∠DCB= ![]() ∠OCB=45°,
∠OCB=45°,
∴HG=HD+DG=HO+BG
(3)解:四边形AEBD可为矩形.
如图,连接BD、DA、AE、EB, 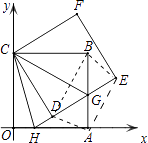
四边形AEBD若为矩形,则需先为平行四边形,即要对角线互相平分,合适的点只有G为AB中点的时候.
∵DG=BG,
∴DG=AG=EG=BG,即平行四边形AEBD对角线相等,则其为矩形,
∴当G点为AB中点时,四边形AEBD为矩形.
∵四边形DAEB为矩形,
∴AG=EG=BG=DG.
∵AB=6,
∴AG=BG=3.
设H点的坐标为(x,0),则HO=x
∵OH=DH,BG=DG,
∴HD=x,DG=3.
在Rt△HGA中,
∵HG=x+3,GA=3,HA=6﹣x,
∴(x+3)2=32+(6﹣x)2,解得x=2.
∴H点的坐标为(2,0).
【解析】(1)根据旋转的性质正方形ABCO绕点C旋转得到正方形CDEF,,得到对应边、对应角相等,得到△CDG≌△CBG;(2)由(1)知△CDG≌△CBG,得到对应边、对应角相等,得到△CHO≌△CHD,根据全等三角形的对应边、对应角相等,得到∠OCH=∠DCH,OH=DH,由正方形的性质,得到HG=HD+DG=HO+BG;(3)根据四边形AEBD若为矩形,则需先为平行四边形,即要对角线互相平分,合适的点只有G为AB中点的时候,由DG=BG,得到DG=AG=EG=BG,即平行四边形AEBD对角线相等,则其为矩形,当G点为AB中点时,四边形AEBD为矩形;再根据勾股定理求出H点的坐标.
【考点精析】根据题目的已知条件,利用正方形的性质的相关知识可以得到问题的答案,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
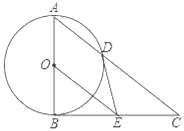
【题目】如图,AB为⊙O直径,BC为⊙O切线,连接A、C两点,交⊙O于点D,BE=CE,连接DE,OE.
(1)判断DE与⊙O的位置关系,并说明理由;
(2)求证:BC2=CD2OE;
(3)若cos∠BAD=![]() ,BE=6,求OE的长.
,BE=6,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,若∠B=60°,点E、F分别在AB、AD上,且BE=AF,则∠AEC+∠AFC的度数等于( )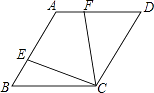
A.120°
B.140°
C.160°
D.180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,出租车是人们出行的一种便利交通工具,折线ABC是在我市乘出租车所付车费y(元)与行车里程x(km)之间的函数关系图象.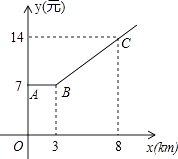
(1)根据图象,当x≥3时y为x的一次函数,请写出函数关系式;
(2)某人乘坐13km,应付多少钱?
(3)若某人付车费42元,出租车行驶了多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南方A市欲将一批容易变质的水果运往B市销售,若有飞机、火车、汽车三种运输方式,现只选择其中一种,这三种运输方式的主要参考数据如下表所示:
运输工具 | 途中速度(km/h) | 途中费用(元/km) | 装卸费用(元) | 装卸时间 |
飞机 | 200 | 16 | 1000 | 2 |
火车 | 100 | 4 | 2000 | 4 |
汽车 | 50 | 8 | 1000 | 2 |
若这批水果在运输(包括装卸)过程中的损耗为200元/h,记A、B两市间的距离为xkm.
(1)如果用W1、W2、W3分别表示使用飞机、火车、汽车运输时的总支出费用(包括损耗),求W1、W2、W3与x间的关系式;
(2)当x=250时,应采用哪种运输方式,才使运输时的总支出费用最小?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】方格纸中小正方形的顶点叫格点.点A和点B是格点,位置如图.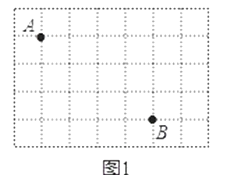
(1)在图1中确定格点C使△ABC为直角三角形,画出一个这样的△ABC;
(2)在图2中确定格点D使△ABD为等腰三角形,画出一个这样的△ABD;
(3)在图2中满足题(2)条件的格点D有个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:
①有理数和数轴上的点一一对应;
②成轴对称的两个图形是全等图形;
③- ![]() 是17的平方根;
是17的平方根;
④等腰三角形的高线、中线及角平分线重合.
其中正确的有( )
A.0个
B.1
C.2个
D.3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com