
【题目】综合探究:如图1,在平面直角坐标系xOy中,抛物线y=﹣ ![]() 与x轴交于点A(﹣6,0)和点B(点A在点B左侧),与y轴交于点C,点P为线段AO上的一个动点,过点P作x轴的垂线l与抛物线交于点E,连接AE,EC.
与x轴交于点A(﹣6,0)和点B(点A在点B左侧),与y轴交于点C,点P为线段AO上的一个动点,过点P作x轴的垂线l与抛物线交于点E,连接AE,EC.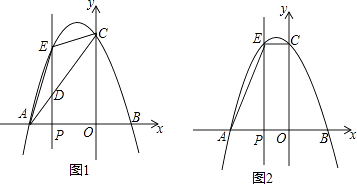
(1)求抛物线的表达式及点C的坐标;
(2)连接AC交直线l于点D,则在点P运动过程中,当点D为EP中点时,S△ADP:S△CDE=;
(3)如图2,当EC∥x轴时,点P停止运动,此时,在抛物线上是否存在点G,使得以点A,E,G为顶点的三角形是直角三角形?若存在,请求出点G的坐标,若不存在,说明理由.
【答案】
(1)
解:∵点A(﹣6,0)在抛物线y=﹣ ![]() x2+bx+8上,
x2+bx+8上,
∴0=﹣ ![]() (﹣6)2+b(﹣6)+8,
(﹣6)2+b(﹣6)+8,
∴b=﹣ ![]() ,
,
∴y=﹣ ![]() x2﹣
x2﹣ ![]() x+8,
x+8,
令x=0,y=8,
∴C(0,8)
(2)1:2
(3)
解:存在点G使得以点A,E,G为顶点的三角形为直角三角形,
连接EG,AG,作GM⊥l,GN⊥x轴,
∵EC∥x轴,
∴EP=CO=8,
把y=8代入y=﹣ ![]() x2﹣
x2﹣ ![]() x+8,
x+8,
∴8=﹣ ![]() x2﹣
x2﹣ ![]() x+8,
x+8,
∴x=0(舍),或x=﹣2,
∴P(﹣2,0),
∴AP=AO﹣PO=4,
Ⅰ、如图1,
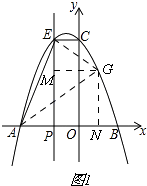
当∠AEG=90°时,
∴∠MEG+∠AEP=90°,
∵∠AEP+∠EAP=90°,
∴∠MEG=∠EAP,
∵∠APE=∠EMG=90°,
∴△EMG∽△APE,
∴ ![]() ,
,
设点G(m,﹣ ![]() m2﹣
m2﹣ ![]() m+8)(m>0),
m+8)(m>0),
∴GN=MP=﹣ ![]() m2﹣
m2﹣ ![]() m+8,
m+8,
∴EM=EP﹣MP=8﹣(﹣ ![]() m2﹣
m2﹣ ![]() m+8)=y=
m+8)=y= ![]() m2+
m2+ ![]() m,
m,
MG=PN=PO+ON=2+m,
∵ ![]() ,
,
∴ ![]() ,
,
∴m=﹣2(舍)或m= ![]() ,
,
∴G( ![]() ,
, ![]() );
);
Ⅱ、如图2,
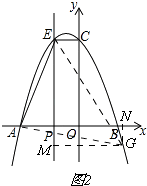
当∠EAG=90°时,
∴∠NAG+∠EAP=90°,
∵∠AEP+∠EAP=90°,
∴∠NAG=∠AEP,
∵∠APE=∠GNA=90°,
∴△GNA∽△APE,
∴ ![]() ,
,
设点G(n,﹣ ![]() n2﹣
n2﹣ ![]() n+8)(n>0,﹣
n+8)(n>0,﹣ ![]() n2﹣
n2﹣ ![]() n+8<0),
n+8<0),
∴GN= ![]() m2+
m2+ ![]() m+8,
m+8,
∴AN=AO+ON=6+n,
∵ ![]() ,
,
∴ ![]() ,
,
∴n=﹣6(舍),或n= ![]() ,
,
∴G( ![]() ,﹣
,﹣ ![]() ),
),
符合条件的G点的坐标为G( ![]() ,
, ![]() )或G(
)或G( ![]() ,﹣
,﹣ ![]() )
)
【解析】解:(2)设E(m,﹣ ![]() m2﹣
m2﹣ ![]() m+8),
m+8),
∴P(m,0),
∵点D为EP中点,
∴DP=DE,D(m,﹣ ![]() m2+﹣
m2+﹣ ![]() x+4),
x+4),
∵A(﹣6,0),C(0,8),
∴直线AC解析式为y= ![]() x+8,
x+8,
∵点D在直线AC上,
∴ ![]() m+8=﹣
m+8=﹣ ![]() m2+﹣
m2+﹣ ![]() x+4,
x+4,
∴m=﹣6(舍)或m=﹣4,
∴P(﹣4,0)
∴AP=2,OP=4,
∴ 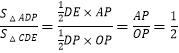 ;
;
所以答案是1:2(1)用待定系数法求出抛物线解析式,令x=0求出y轴交点坐标;(2)先确定出直线AC解析式为y= ![]() x+8,设出点E的坐标,表示出点D(m,﹣
x+8,设出点E的坐标,表示出点D(m,﹣ ![]() m2+﹣
m2+﹣ ![]() x+4),而点D在直线AC上,列出方程
x+4),而点D在直线AC上,列出方程 ![]() m+8=﹣
m+8=﹣ ![]() m2+﹣
m2+﹣ ![]() x+4,求出m,从而得出结论;(3)先求出点P的坐标,再分两种情况计算Ⅰ、当∠AEG=90°时,判断出△EMG∽△APE,得出比例式求解即可,Ⅱ、当∠EAG=90°时,判断出△GNA∽△APE,得到比例式计算.
x+4,求出m,从而得出结论;(3)先求出点P的坐标,再分两种情况计算Ⅰ、当∠AEG=90°时,判断出△EMG∽△APE,得出比例式求解即可,Ⅱ、当∠EAG=90°时,判断出△GNA∽△APE,得到比例式计算.
【考点精析】掌握二次函数的概念和二次函数的图象是解答本题的根本,需要知道一般地,自变量x和因变量y之间存在如下关系:一般式:y=ax2+bx+c(a≠0,a、b、c为常数),则称y为x的二次函数;二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,O是AB边上的一点,以OA为半径的⊙O与边BC相切于点E. 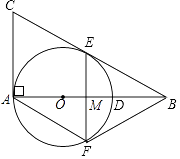
(1)若AC=6,BC=10,求⊙O的半径.
(2)过点E作弦EF⊥AB于M,连接AF,若∠F=2∠B,求证:四边形ACEF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,AC与BD相交于点O,AC=BC,点E在DC的延长线上,∠BEC=∠ACB,已知BC=9,cos∠ABC= ![]() .
.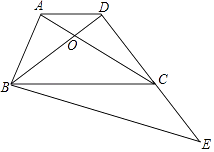
(1)求证:BC2=CDBE;
(2)设AD=x,CE=y,求y与x之间的函数解析式,并写出定义域;
(3)如果△DBC∽△DEB,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+ ![]() 的图象与y轴交于点A(0,4),与x轴交于点B,C,点C坐标为(8,0),连AB,AC,点N在线段BC上运动(不与点B,C重合)过点N作NM∥AC,交AB于点M.
的图象与y轴交于点A(0,4),与x轴交于点B,C,点C坐标为(8,0),连AB,AC,点N在线段BC上运动(不与点B,C重合)过点N作NM∥AC,交AB于点M.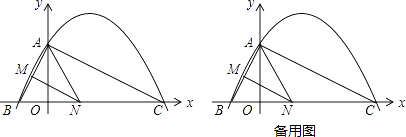
(1)判断△ABC的形状,并说明理由;
(2)当以点A,M,N为顶点的三角形与以点A,B,O为顶点的三角形相似时,求点N的坐标;
(3)当△AMN面积等于3时,直接写出此时点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校积极倡导学生展示自我,发展综合素质,在新学期举办的校园文化艺术节中,学生可以在舞蹈、器乐、声乐、小品、播音主持五个类别中挑选一项报名参加比赛,八年级学生小明从本年级学生各个类别的报名登记表中随机抽取了一部分学生的报名情况进行整理,并制作了如下不完整的条形统计图和扇形统计图,请解答下列问题: 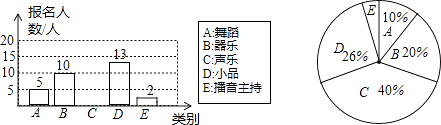
(1)小明随机抽取了名学生的报名情况进行整理,扇形统计图中,表示E类别部分的扇形的圆心角度数为度;
(2)将条形统计图补充完整;
(3)小华认为如果知道八年级报名参加比赛的总人数,则根据小明制作的统计图就可以估算出八年级报名参加声乐比赛的人数.小明认为如果知道初中三个年级报名参加比赛的总人数,则根据自己制作的统计图也可以估算出整个初中年级报名参见声乐比赛的人数.你认为他俩的看法对吗?并说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点O为坐标原点,A、B、C三点的坐标为( ![]() ,0)、(3
,0)、(3 ![]() ,0)、(0,5),点D在第一象限,且∠ADB=60°,则线段CD的长的最小值为 .
,0)、(0,5),点D在第一象限,且∠ADB=60°,则线段CD的长的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1、2是底面半径为1cm,母线长为2cm的圆柱体和圆锥体模型.现要用长为2πcm,宽为4cm的长方形彩纸(如图3)装饰圆柱、圆锥模型表面.已知一个圆柱和一个圆锥模型为一套,长方形彩纸共有122张,用这些纸最多能装饰多少套模型呢? 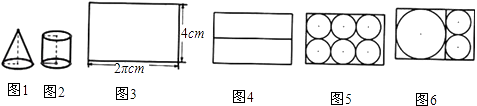 老师:“长方形纸可以怎么裁剪呢?”
老师:“长方形纸可以怎么裁剪呢?”
学生甲:“可按图4方式裁剪出2张长方形.”
学生乙:“可按图5方式裁剪出6个小圆.”
学生丙:“可按图6方式裁剪出1个大圆和2个小圆.”
老师:尽管还有其他裁剪方法,但为裁剪方便,我们就仅用这三位同学的裁剪方法!
(1)计算:圆柱的侧面积是cm2 , 圆锥的侧面积是cm2 .
(2)1张长方形彩纸剪拼后最多能装饰个圆锥模型;5张长方形彩纸剪拼后最多能装饰个圆柱体模型.
(3)求用122张彩纸对多能装饰的圆锥、圆柱模型套数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐际系xOy中,当m,n满足mn=k(k为常数,且m>0,n>0)时,就称点(m,n)为“等积点”.
(1)若k=4,求函数y=x﹣4的图象上满足条件的,“等积点”坐标;
(2)若直线y=﹣x+b(b>0)与x轴、y轴分别交于点A和点B,并且直线有且只有一个“等积点”,过点A与y轴平行的直线和过点B与x轴平行的直线交于点C,点E是直线AC上的“等积点”,点F是直线BC上的“等积点”,若△OEF的面积为k2+ ![]() k﹣
k﹣ ![]() ,求EF的值.
,求EF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD和矩形EFGO在平面直角坐标系中,点B,F的坐标分别为(﹣4,4),(2,1).若矩形ABCD和矩形EFGO是位似图形,点P(点P在GC上)是位似中心,则点P的坐标为( ) 
A.(0,3)
B.(0,2.5)
C.(0,2)
D.(0,1.5)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com