
����Ŀ�����ھ���ABCD�У�AB=4��BC=8�������Խ��߽���O��ֱ��EF�Ƶ�O��ת���ֱ�AD��BC�ڵ�E��F������AF��CE��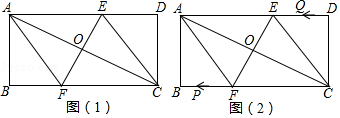
��1����ͼ��1��������������������ͨ�ı��Ρ����Ρ���ͨƽ���ı��Ρ������λ���������ѡ����գ���ת�������ı���AFCEʼ��Ϊ��
����EΪAD���е�ʱ�ı���AFCEΪ��
��EF��ACʱ�ı���AFCEΪ��
��2����ͼ��1������EF��ACʱ����AF�ij���
��3����ͼ��2�����ڣ�2���Ļ����ϣ�������P��A���������A��F��B��A�˶�һ��ֹͣ���ٶ�Ϊÿ��5���ף�ͬʱ��Q��C���������C��D��E��C�˶�һ��ֹͣ���ٶ�Ϊÿ��4���ף���P��Q�˶������У��ڼ���ʱ���ı���APCQ��ƽ���ı��Σ�
���𰸡�
��1��ƽ���ı��Σ�ƽ���ı��Σ�����
��2��
�⣺�������εı߳�AF=CF=xcm����BF=��8��x��cm��
��Rt��ABF��AB=4cm��
�ɹ��ɶ����ã�AB2+BF2=AF2��
��42+��8��x��2=x2��
��ã�x=5��
��AF=5
��3��
��������ã�P��AF��ʱ��Q��CD�ϣ���ʱA��C��P��Q�ĵ㲻���ܹ���ƽ���ı��Σ�
ͬ��P��AB��ʱ��Q��DE��CE�ϣ�Ҳ���ܹ���ƽ���ı��Σ�
��ֻ�е�P����BF�ϣ�Q����ED��ʱ�����ܹ���ƽ���ı��Σ�
����A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı���ʱ��
PC=QA��
�ߵ�P���ٶ�Ϊÿ��5cm����Q���ٶ�Ϊÿ��4cm���˶�ʱ��Ϊt�룬
��PC=5t��QA=12��4t��
��5t=12��4t��
��ã�t= ![]() ��
��
����A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı���ʱ��t= ![]() �룮
�룮
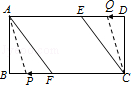
���������⣺��1������EΪAD���е�ʱ���ı���AFCEΪƽ���ı��Σ��������£�
���ı���ABCD�Ǿ��Σ�
��AD��BC��OA=OC��
���CAD=��ACB����AEF=��CFE��
�ڡ�AOE�͡�COF�У� 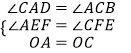 ��
��
���AOE�ա�COF��AAS����
��AE=CF��
�֡�AE��CF��
���ı���AFCEΪƽ���ı��Σ�
����EΪAD���е�ʱ��AE=CF��AE��CF��
���ı���AFCEΪƽ���ı��Σ�
��EF��ACʱ���ı���AFCEΪ���Σ��������£�
���ɢ�֪�ı���AFCEΪƽ���ı��Σ�
��EF��AC��
���ı���AFCEΪ���Σ�
���Դ��ǣ�ƽ���ı��Σ�ƽ���ı��Σ����Σ�
�����㾫����������Ĺؼ���������ɶ����ĸ�������֪ʶ������ֱ����������ֱ�DZ�a��b��ƽ���͵���б��c��ƽ��,��;a2+b2=c2���Լ���ƽ���ı��ε����ʵ����⣬�˽�ƽ���ı��εĶԱ������ƽ�У�ƽ���ı��εĶԽ���ȣ��ڽǻ�����ƽ���ı��εĶԽ�����ƽ�֣�


 ��ѧ��ʦ����ϵ�д�
��ѧ��ʦ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����е��������ij�����ԭ��ÿ��xԪ����һ�ν��۴��ۡ����ڶ��ν���ÿ���ּ�10Ԫ�������ν��ۺ��ۼ�Ϊ90Ԫ����õ����̣� ��
A.0.8x��10=90
B.0.08x��10=90
C.90��0.8x=10
D.x��0.8x��10=90
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�DZ�����һ�ֲ�Ʒ30�������ͼ��Ʒ��������y����λ��������ʱ��t����λ���죩�Ĵ��º�����ϵ��ͼ�٣�ͼ����һ����Ʒ����������z����λ��Ԫ����ʱ��t����λ���죩�ĺ�����ϵ����֪����������=����������һ����Ʒ�������������н����������ǣ� ��

A. ��������Ϊ150�����ǵ�12�����30��
B. ��10������һ����Ʒ��������15Ԫ
C. �ӵ�1�쵽��20�����ʱ���������������������ټ���
D. ��18���������������1225Ԫ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����һ�����鰴��۵ľ��۳��ۣ��Կɻ���20%��������Ľ���Ϊ42Ԫ������Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ�����������������У����ж�AB��CD���ǣ� �� 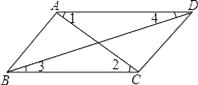
A.��1=��2
B.��ABD=��BDC
C.��3=��4
D.��BAD+��ABC=180��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AD��BC������ΪD����B=60�㣬��C=45�㣮 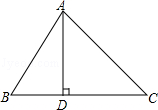
��1�����BAC�Ķ�����
��2����AD=2 ![]() ����AC��AB�ij���
����AC��AB�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ������Ȥ�С����Χ��һ����������������һ�߿�ǽ�����������ɳ�Ϊ30�����Χ�ɣ���֪ǽ��Ϊ18�ף���ͼ��ʾ���������������ֱ��ǽ��һ�߳�Ϊx�ף�
��1�������������Ϊ72ƽ���ף���x��
��2����ƽ����ǽ��һ�߳���С��8�ף������������������ֵ����Сֵ������У�������ֵ����Сֵ�����û�У���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
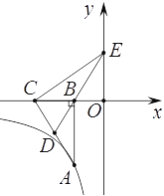
����Ŀ����ͼ����֪��A�ڷ���������![]() �ϣ���Rt��ABC����DΪб��AC���е㣬��DB���ӳ���y���ڵ�E������BCE�����Ϊ8��
�ϣ���Rt��ABC����DΪб��AC���е㣬��DB���ӳ���y���ڵ�E������BCE�����Ϊ8��
��1����֤����EOB�ס�ABC��
��2�����������Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AC����O��ֱ����BC����O���ң���P����O��һ�㣬����PA��PB��AB����֪��PBA=��C��

��1����֤��PB����O�����ߣ�
��2������OP����OP��BC����OP=8����O�İ뾶Ϊ![]() ����BC�ij���
����BC�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com