
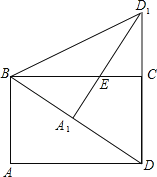
【题目】矩形ABCD中,∠DBA=60°,把△ABD绕点B逆时针旋转使得点A落在BD上,点A对称点为点A1,点D对称点为点D1,A1 D1与BC交于点E,连接D1C.

(1)求证:EC=EA1;
(2)求证:点D1、C、D在同一直线上.
【答案】见解析
【解析】
试题分析:(1)利用矩形的性质得∠ADB=∠DBC=30°,AD=BC,再根据旋转的性质得∠A1 BD1=∠ABD=60°,A1 D1=AD=BC,∠BD1 A1=∠ADB=30°,则∠D1B C=∠A1 BD1﹣∠DBC=30°,于是根据等腰三角形的判定得BE=ED1,所以EC=E A1;
(2)利用“SAS”可证明△B E A1≌△∠CED1,则∠D1CE=∠B A1 E=90°,所以∠D1CE+∠BCD=180°,于是可判断点D1、C、D在同一直线上.
(1)证明:∵矩形ABCD中,∠DBA=60°,
∴∠ADB=∠DBC=30°,AD=BC,
∵△BA1 D1是△ABD绕点B逆时针旋转所得,且点A落在BD上,
∴∠A1 BD1=∠ABD=60°,A1 D1=AD=BC,∠BD1 A1=∠ADB=30°,
∴∠D1B C=∠A1 BD1﹣∠DBC=60°﹣30°=30°,
∴∠D1B E=∠ED1B,
∴BE=ED1,
∴BC﹣BE=A1 D1﹣ED1,
∴EC=E A1;
(2)证明:在△B E A1和△∠CED1 中,
 ,
,
∴△B E A1≌△∠CED1,
∴∠D1CE=∠B A1 E=90°,
∴∠D1CE+∠BCD=90°+90°=180°,
∴点D1、C、D在同一直线上.


科目:初中数学 来源: 题型:
【题目】将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上.另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图,则三角板的最大边的长为( )
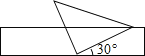
A.3cm B.6cm C.![]() cm D.
cm D.![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据电力部门统计,每天8:00至21:00是用电的高峰期,简称“峰时”,21:00至次日8:00是用电的低谷时期,简称“谷时”,为了缓解供电需求紧张矛盾,某市电力部门于本月初统一换装“峰谷分时”电表,对用电实行“峰谷分时电价”新政策,具体见下表:

(1)小张家上月“峰时”用电50度,“谷时”用电20度,若上月初换表,则相对于换表前小张家的电费是增多了还是减少了?增多或减少了多少元?请说明理由.
(2)小张家这个月用电95度,经测算比换表前使用95度电节省了5.9元,问小张家这个月使用“峰时电”和“谷时电”分别是多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC、AB,分别交于点D、E,且∠CBD=∠A;

(1)判断直线BD与⊙O的位置关系,并证明你的结论;
(2)若AD:AO=6:5,BC=2,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,AC=BC,∠ACB=90゜,点P在射线AC上,连接PB,将线段PB绕点B逆时针旋转90゜得线段BN,AN交直线BC于M.
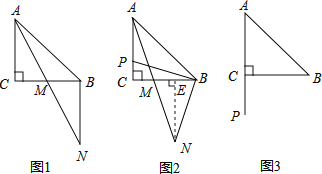
(1)如图1.若点P与点C重合,则![]() = ,
= ,![]() = (直接写出结果):
= (直接写出结果):
(2)如图2,若点P在线段AC上,求证:AP=2MC;
(3)如图3,若点P在线段AC的延长线上,完成图形,并直接写出![]() = .
= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com