
【题目】已知△ABC中,AC=BC,∠ACB=90゜,点P在射线AC上,连接PB,将线段PB绕点B逆时针旋转90゜得线段BN,AN交直线BC于M.
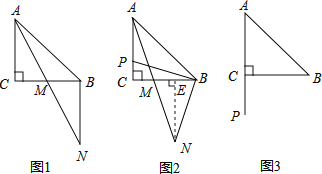
(1)如图1.若点P与点C重合,则![]() = ,
= ,![]() = (直接写出结果):
= (直接写出结果):
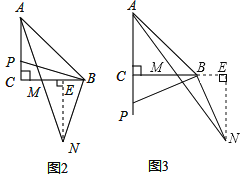
(2)如图2,若点P在线段AC上,求证:AP=2MC;
(3)如图3,若点P在线段AC的延长线上,完成图形,并直接写出![]() = .
= .
【答案】(1)1,![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() .
.
【解析】
试题分析:(1)先求出∠C=∠CBN,再利用“角角边”证明△ACM和△NBM全等,根据全等三角形对应边相等可得AM=MN,MC=MB,再求出AP=AC=2MC,然后求解即可;
(2)过点N作NE⊥BC于E,根据同角的余角相等求出∠PBC=∠BNE,然后利用“角角边”证明△PBC和△BNE全等,根据全等三角形对应边相等可得BE=PC,NE=BC,然后求出AP=CE,AC=NE,再利用“角角边”证明△ACM和△NEM全等根据全等三角形对应边相等可得MC=ME,整理即可得证;
(3)过点N作NE⊥BC交CB的延长线于E,然后与(2)的求解方法相同.
(1)解:∵线段PB绕点B逆时针旋转90゜得线段BN,
∴∠CBN=90°,BC=BN,
∴∠C=∠CBN,AC=BN,
在△ACM和△NBM中,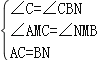 ,
,
∴△ACM≌△NBM(AAS),
∴AM=MN,MC=MB,
∴AP=AC=BC=MC+MB=2MC,
∴![]() =1,
=1,![]() =
=![]() ;
;
(2)证明:如图2,过点N作NE⊥BC于E,
∴∠BNE+∠CBN=90°,
∵线段PB绕点B逆时针旋转90゜得线段BN,
∴∠PBC+∠CBN=90°,
∴∠PBC=∠BNE,
在△PBC和△BNE中,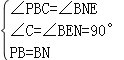 ,
,
∴△PBC≌△BNE(AAS),
∴BE=PC,NE=BC,
∴AP=AC﹣PC=BC﹣BE=CE,AC=NE,
在△ACM和△NEM中,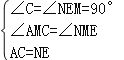 ,
,
∴△ACM≌△NEM(AAS),
∴MC=ME,
∴CE=2MC,
∴AP=2MC;
(3)解:如图3,过点N作NE⊥BC交CB的延长线于E,过点N作NE⊥BC于E,
∴∠BNE+∠CBN=90°,
∵线段PB绕点B逆时针旋转90゜得线段BN,
∴∠PBC+∠CBN=90°,
∴∠PBC=∠BNE,
在△PBC和△BNE中,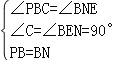 ,
,
∴△PBC≌△BNE(AAS),
∴BE=PC,NE=BC,
∴AP=AC﹣PC=BC﹣BE=CE,AC=NE,
在△ACM和△NEM中,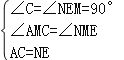 ,
,
∴△ACM≌△NEM(AAS),
∴MC=ME,
∵AP=AC+PC,
CE=BC+BE=2MC,
∴AP=CE=2MC,
∴![]() =
=![]() .
.
故答案为:(1)1,![]() ;(3)
;(3)![]() .
.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】矩形ABCD中,∠DBA=60°,把△ABD绕点B逆时针旋转使得点A落在BD上,点A对称点为点A1,点D对称点为点D1,A1 D1与BC交于点E,连接D1C.

(1)求证:EC=EA1;
(2)求证:点D1、C、D在同一直线上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个等边三角形木框,甲虫P在边框AC上爬行(A,C端点除外),设甲虫P到另外两边的距离之和为d,等边三角形ABC的高为h,则d与h的大小关系是( )
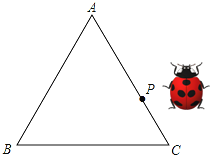
A.d>h B.d<h C.d=h D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解一批产品的质量,从中抽取300个产品进行检验,在这个问题中,被抽取的300个产品叫做( )
A. 总体 B. 个体 C. 总体的一个样本 D. 普查方式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】肥皂泡的泡壁厚度大约是0.0007mm,0.0007用科学记数法表示为( )
A. 0.7×10﹣3 B. 7×10﹣3 C. 7×10﹣4 D. 7×10﹣5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次消防演习中,消防员架起一架25米长的云梯,如图斜靠在一面墙上,梯子底端离墙7米.
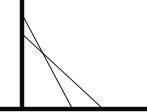
(1)求这个梯子的顶端距地面有多高?
(2)如果消防员接到命令,要求梯子的顶端下降4米(云梯长度不变),那么云梯的底部在水平方向应滑动多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用反证法证明命题:“若a,b是整数,ab能被3整除,那么a,b中至少有一个能被3整除”时,假设应为( )
A. a,b都能被3整除 B. a不能被3整除 C. a,b不都能被3整除 D. a,b都不能被3整除
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com