
【题目】如图,抛物线y=ax2+bx﹣a﹣b(a<0,a、b为常数)与x轴交于A、C两点,与y轴交于B点,直线AB的函数关系式为y= ![]() x+
x+ ![]() .
.
(1)求该抛物线的函数关系式与C点坐标;
(2)已知点M(m,0)是线段OA上的一个动点,过点M作x轴的垂线l分别与直线AB和抛物线交于D、E两点,当m为何值时,△BDE恰好是以DE为底边的等腰三角形?
(3)在(2)问条件下,当△BDE恰好是以DE为底边的等腰三角形时,动点M相应位置记为点M′,将OM′绕原点O顺时针旋转得到ON(旋转角在0°到90°之间);
i:探究:线段OB上是否存在定点P(P不与O、B重合),无论ON如何旋转, ![]() 始终保持不变,若存在,试求出P点坐标;若不存在,请说明理由;
始终保持不变,若存在,试求出P点坐标;若不存在,请说明理由;
ii:试求出此旋转过程中,(NA+ ![]() NB)的最小值.
NB)的最小值.
【答案】
(1)
解:在y= ![]() x+
x+ ![]() 中,令x=0,则y=
中,令x=0,则y= ![]() ,令y=0,则x=﹣6,
,令y=0,则x=﹣6,
∴B(0, ![]() ),A(﹣6,0),
),A(﹣6,0),
把B(0, ![]() ),A(﹣6,0)代入y=ax2+bx﹣a﹣b得
),A(﹣6,0)代入y=ax2+bx﹣a﹣b得  ,
,
∴  ,
,
∴抛物线的函数关系式为:y=﹣ ![]() x2﹣
x2﹣ ![]() x+
x+ ![]() ,
,
令y=0,则=﹣ ![]() x2﹣
x2﹣ ![]() x+
x+ ![]() =0,
=0,
∴x1=﹣6,x2=1,
∴C(1,0)
(2)
解:∵点M(m,0),过点M作x轴的垂线l分别与直线AB和抛物线交于D、E两点,
∴D(m, ![]() m+
m+ ![]() ),当DE为底时,
),当DE为底时,
作BG⊥DE于G,则EG=GD= ![]() ED,GM=OB=
ED,GM=OB= ![]() ,
,
∴ ![]() m+
m+ ![]() (﹣
(﹣ ![]() m2﹣
m2﹣ ![]() m+
m+ ![]() +
+ ![]() m+
m+ ![]() )=
)= ![]() ,
,
解得:m1=﹣4,m2=9(不合题意,舍去),
∴当m=﹣4时,△BDE恰好是以DE为底边的等腰三角形

(3)
解:i:存在,
∵ON=OM′=4,OB= ![]() ,
,
∵∠NOP=∠BON,
∴当△NOP∽△BON时, ![]() =
= ![]() ,
,
∴ ![]() 不变,
不变,
即OP= ![]() =3,
=3,
∴P(0,3)
ii:∵N在以O为圆心,4为半径的半圆上,由(i)知, ![]() =
= ![]() ,
,
∴NP= ![]() NB,
NB,
∴(NA+ ![]() NB)的最小值=NA+NP,
NB)的最小值=NA+NP,
∴此时N,A,P三点共线,
∴(NA+ ![]() NB)的最小值=
NB)的最小值= ![]() =3
=3 ![]() .
.

【解析】(1)根据已知条件得到B(0, ![]() ),A(﹣6,0),解方程组得到抛物线的函数关系式为:y=﹣
),A(﹣6,0),解方程组得到抛物线的函数关系式为:y=﹣ ![]() x2﹣
x2﹣ ![]() x+
x+ ![]() ,于是得到C(1,0);(2)由点M(m,0),过点M作x轴的垂线l分别与直线AB和抛物线交于D、E两点,得到D(m,
,于是得到C(1,0);(2)由点M(m,0),过点M作x轴的垂线l分别与直线AB和抛物线交于D、E两点,得到D(m, ![]() m+
m+ ![]() ),当DE为底时,作BG⊥DE于G,根据等腰三角形的性质得到EG=GD=
),当DE为底时,作BG⊥DE于G,根据等腰三角形的性质得到EG=GD= ![]() ED,GM=OB=
ED,GM=OB= ![]() ,列方程即可得到结论;(3)i:根据已知条件得到ON=OM′=4,OB=
,列方程即可得到结论;(3)i:根据已知条件得到ON=OM′=4,OB= ![]() ,由∠NOP=∠BON,特殊的当△NOP∽△BON时,根据相似三角形的性质得到
,由∠NOP=∠BON,特殊的当△NOP∽△BON时,根据相似三角形的性质得到 ![]() =
= ![]() ,于是得到结论;
,于是得到结论;
ii:根据题意得到N在以O为圆心,4为半径的半圆上,由(i)知, ![]() =
= ![]() ,得到NP=
,得到NP= ![]() NB,于是得到(NA+
NB,于是得到(NA+ ![]() NB)的最小值=NA+NP,此时N,A,P三点共线,根据勾股定理得到结论.
NB)的最小值=NA+NP,此时N,A,P三点共线,根据勾股定理得到结论.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C为⊙O上一点,AD与过点C的切线互相垂直,垂足为点D,AD交⊙O于点E,连接CE,CB. 
(1)求证:CE=CB;
(2)若AC=2 ![]() ,CE=
,CE= ![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB≠AC.D、E分别为边AB、AC上的点.AC=3AD,AB=3AE,点F为BC边上一点,添加一个条件: , 可以使得△FDB与△ADE相似.(只需写出一个) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=mx2﹣16mx+48m(m>0)与x轴交于A,B两点(点B在点A左侧),与y轴交于点C,点D是抛物线上的一个动点,且位于第四象限,连接OD、BD、AC、AD,延长AD交y轴于点E.
(1)若△OAC为等腰直角三角形,求m的值;
(2)若对任意m>0,C、E两点总关于原点对称,求点D的坐标(用含m的式子表示);
(3)当点D运动到某一位置时,恰好使得∠ODB=∠OAD,且点D为线段AE的中点,此时对于该抛物线上任意一点P(x0 , y0)总有n+ ![]() ≥﹣4
≥﹣4 ![]() my02﹣12
my02﹣12 ![]() y0﹣50成立,求实数n的最小值.
y0﹣50成立,求实数n的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乌江快铁大桥是快铁渝黔线的一项重要工程,由主桥AB和引桥BC两部分组成(如图所示),建造前工程师用以下方式做了测量;无人机在A处正上方97m处的P点,测得B处的俯角为30°(当时C处被小山体阻挡无法观测),无人机飞行到B处正上方的D处时能看到C处,此时测得C处俯角为80°36′.
(长度均精确到1m,参考数据: ![]() ≈1.73,sin80°36′≈0.987,cos80°36′≈0.163,tan80°36′≈6.06)
≈1.73,sin80°36′≈0.987,cos80°36′≈0.163,tan80°36′≈6.06)
(1)求主桥AB的长度;
(2)若两观察点P、D的连线与水平方向的夹角为30°,求引桥BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“一带一路”倡议下,我国已成为设施联通,贸易畅通的促进者,同时也带动了我国与沿线国家的货物交换的增速发展,如图是湘成物流园2016年通过“海、陆(汽车)、空、铁”四种模式运输货物的统计图. 请根据统计图解决下面的问题:
(1)该物流园2016年货运总量是多少万吨?
(2)该物流园2016年空运货物的总量是多少万吨?并补全条形统计图;
(3)求条形统计图中陆运货物量对应的扇形圆心角的度数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB的一边OA为平面镜,∠AOB=38°,在OB上有一点E , 从E点射出一束光线经OA上一点D反射,反射光线DC恰好与OB平行,则∠DEB的度数是( )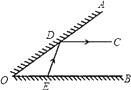
A.76°
B.52°
C.45°
D.38°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店尝试用单价随天数而变化的销售模式销售一种商品,利用30天的时间销售一种成本为10元/件的商品售后,经过统计得到此商品单价在第x天(x为正整数)销售的相关信息,如表所示:
销售量n(件) | n=50﹣x |
销售单价m(元/件) | 当1≤x≤20时, |
当21≤x≤30时, |
(1)请计算第15天该商品单价为多少元/件?
(2)求网店销售该商品30天里所获利润y(元)关于x(天)的函数关系式;
(3)这30天中第几天获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,AD∥BC,AD=AB=DC= ![]() BC=1,E是PC的中点,面PAC⊥面ABCD.
BC=1,E是PC的中点,面PAC⊥面ABCD. 
(Ⅰ)证明:ED∥面PAB;
(Ⅱ)若PC=2,PA= ![]() ,求二面角A﹣PC﹣D的余弦值.
,求二面角A﹣PC﹣D的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com