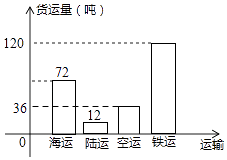
【题目】在“一带一路”倡议下，我国已成为设施联通，贸易畅通的促进者，同时也带动了我国与沿线国家的货物交换的增速发展，如图是湘成物流园2016年通过“海、陆（汽车）、空、铁”四种模式运输货物的统计图． 请根据统计图解决下面的问题：

（1）该物流园2016年货运总量是多少万吨？
（2）该物流园2016年空运货物的总量是多少万吨？并补全条形统计图；
（3）求条形统计图中陆运货物量对应的扇形圆心角的度数

参考答案：

【答案】
（1）解：2016年货运总量是120÷50%=240吨
（2）解：2016年空运货物的总量是240×15%=36吨，

条形统计图如下：


（3）解：陆运货物量对应的扇形圆心角的度数为 ×360°=18°
【解析】（1）根据铁运的货运量以及百分比，即可得到物流园2016年货运总量；（2）根据空运的百分比，即可得到物流园2016年空运货物的总量，并据此补全条形统计图；（3）根据陆运的百分比乘上360°，即可得到陆运货物量对应的扇形圆心角的度数．
【考点精析】认真审题，首先需要了解扇形统计图(能清楚地表示出各部分在总体中所占的百分比．但是不能清楚地表示出每个项目的具体数目以及事物的变化情况)，还要掌握条形统计图(能清楚地表示出每个项目的具体数目，但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况)的相关知识才是答题的关键．

关闭