
����Ŀ����ͼ����֪�����ߵĶԳ�����y�ᣬ�ҵ㣨2��2������1�� ![]() �����������ϣ���P���������ϲ��붥��N�غϵ�һ���㣬��P��PA��x����A��PC��y����C���ӳ�PC����������E����M��O���������߶���N�ĶԳƵ㣬D��C�����N�ĶԳƵ㣮
�����������ϣ���P���������ϲ��붥��N�غϵ�һ���㣬��P��PA��x����A��PC��y����C���ӳ�PC����������E����M��O���������߶���N�ĶԳƵ㣬D��C�����N�ĶԳƵ㣮
��1���������ߵĽ���ʽ������N�����ꣻ
��2����֤���ı���PMDA��ƽ���ı��Σ�
��3����֤����DPE�ס�PAM������������ǵ����Ʊ�Ϊ ![]() ʱ�ĵ�P�����꣮
ʱ�ĵ�P�����꣮
���𰸡�
��1��
�⣺�������ߵĶԳ�����y�ᣬ
����������߽���ʽΪy=ax2+c��
�ߵ㣨2��2������1�� ![]() �����������ϣ�
�����������ϣ�
�� 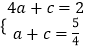 �����
����� ![]() ��
��
�������߽���ʽΪy= ![]() x2+1��
x2+1��
��N��������0��1��
��2��
֤������P��t�� ![]() t2+1������C��0��
t2+1������C��0�� ![]() t2+1����PA=
t2+1����PA= ![]() t2+1��
t2+1��
��M��O���������߶���N�ĶԳƵ㣬D��C�����N�ĶԳƵ㣬��N��0��1����
��M��0��2����
��OC= ![]() t2+1��ON=1��
t2+1��ON=1��
��DM=CN= ![]() t2+1��1=
t2+1��1= ![]() t2��
t2��
��OD= ![]() t2��1��
t2��1��
��D��0���� ![]() t2+1����
t2+1����
��DM=2������ ![]() t2+1��=
t2+1��= ![]() t2+1=PA����PM��DM��
t2+1=PA����PM��DM��
���ı���PMDAΪƽ���ı���
��3��
�⣺ͬ��2����P��t�� ![]() t2+1������C��0��
t2+1������C��0�� ![]() t2+1����PA=
t2+1����PA= ![]() t2+1��PC=|t|��
t2+1��PC=|t|��
��M��0��2����
��CM= ![]() t2+1��2=
t2+1��2= ![]() t2��1��
t2��1��
��Rt��PMC�У��ɹ��ɶ����ɵ�PM= ![]() =
= ![]() =
= ![]() =
= ![]() t2+1=PA�����ı���PMDAΪƽ���ı��Σ�
t2+1=PA�����ı���PMDAΪƽ���ı��Σ�
���ı���PMDAΪ���Σ�
���APM=��ADM=2��PDM��
��PE��y�ᣬ�������߶Գ���Ϊy�ᣬ
��DP=DE���ҡ�PDE=2��PDM��
���PDE=��APM���� ![]() =
= ![]() ��
��
���DPE�ס�PAM��
��OA=|t|��OM=2��
��AM= ![]() ����PE=2PC=2|t|��
����PE=2PC=2|t|��
�����Ʊ�Ϊ ![]() ʱ����
ʱ���� ![]() =
= ![]() ����
���� ![]() =
= ![]() �����t=2
�����t=2 ![]() ��t=��2
��t=��2 ![]() ��
��
��P��������2 ![]() ��4����2
��4����2 ![]() ��4��
��4��
����������1������֪������꣬���ô���ϵ��������������ߵĽ���ʽ��������䶥��N�����ꣻ��2����P�������Ϊt����ɱ�ʾ��C��D��M��A�����꣬�Ӷ��ɱ�ʾ��PA��DM�ij�����PA=DM��֤�ý��ۣ���3����P�������Ϊt����Rt��PCM�У��ɱ�ʾ��PM�������PM=PA����֪�ı���PMDAΪ���Σ������ε����ʺ������ߵĶԳ��Կɵá�PDE=��APM����֤�ý��ۣ���Rt��AOM�У���t��ʾ��AM�ij����ٱ�ʾ��PE�ij��������Ʊ�Ϊ ![]() �ɵõ�����t�ķ��̣������t��ֵ�������P�����꣮
�ɵõ�����t�ķ��̣������t��ֵ�������P�����꣮
�����㾫����������Ŀ����֪�������������ε����ʵ����֪ʶ���Եõ�����Ĵ𰸣���Ҫ�������ε������߶���ȣ����εĶԽ����ഹֱ������ÿһ���Խ���ƽ��һ��Խǣ����α������Խ��߷ֳ��ĸ�ȫ�ȵ�ֱ�������Σ����ε�������������Խ��߳��Ļ���һ�룮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ������ǿ��ë������ƹ���������������������˶���ÿλͬѧ������ֻ��ѡ��һ�������˶����Ը�Уѧ�������ȡ10%���е��飬���ݵ��������������²�������Ƶ���ֲ���������ͳ��ͼ��
�˶���Ŀ | Ƶ���������� |
��� | 30 |
���� | a |
ƹ���� | 36 |
���� | b |
���� | 12 |

���������ͼ����Ϣ����������⣺
��1��Ƶ���ֲ����е�a= �� b=��
��2��������ͳ��ͼ�У����������ڵ����ε�Բ�Ľ�Ϊ�ȣ�
��3��ȫУ�ж�����ѧ��ѡ��μ�ƹ�����˶���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ͼ���У�������Գ�ͼ�Σ��������ĶԳ�ͼ�ε��ǣ� ��
A. ֱ��������
ֱ��������
B. �������
�������
C. ������
������
D. ƽ���ı���
ƽ���ı���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���н��ܼ��ţ�������ɫ���У�����3�����������������������׳ơ�С�Ƴ�����������½�������ij�����ij��˾���ڼס��������ֵ�����Ͷ��һ����С�Ƴ������������г�����A��B���ֲ�ͬ���ͣ���ش��������⣺
����1������
�ù�˾�����ڼ����������Ե�Ͷ�ţ���Ͷ��A��B�������г���50����Ͷ�ųɱ�����7500Ԫ������B�ͳ��ijɱ����۱�A�ͳ���10Ԫ��A��B�������г��ĵ��۸��Ƕ��٣�
����2��Ͷ�ŷ�ʽ
�ù�˾������ȡ����Ͷ�ŷ�ʽ������ÿ1000��Ͷ��a����С�Ƴ������ҽ���ÿ1000��Ͷ�� ![]() ����С�Ƴ�������������Ͷ�ŷ�ʽ��������Ͷ��1500�����ҽ�����Ͷ��1200�������������������15���ˣ�����a��ֵ��
����С�Ƴ�������������Ͷ�ŷ�ʽ��������Ͷ��1500�����ҽ�����Ͷ��1200�������������������15���ˣ�����a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�һ��һ·�������£��ҹ��ѳ�Ϊ��ʩ��ͨ��ó�׳�ͨ�Ĵٽ��ߣ�ͬʱҲ�������ҹ������߹��ҵĻ��サ�������ٷ�չ����ͼ���������2016��ͨ��������½�����������ա���������ģʽ��������ͳ��ͼ�� �����ͳ��ͼ�����������⣺
��1��������2016����������Ƕ�����֣�
��2��������2016����˻���������Ƕ�����֣�����ȫ����ͳ��ͼ��
��3��������ͳ��ͼ��½�˻�������Ӧ������Բ�ĽǵĶ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵȱ�������ABC�У�BC=8����D�DZ�AB�㣬��BD=3,��P�DZ�BC��һ���㣬�� ![]() �㣬PE����AC�ڵ�E����CE=ʱ�����������ĵ�P����ֻ��һ����
�㣬PE����AC�ڵ�E����CE=ʱ�����������ĵ�P����ֻ��һ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���۹�˾Ϊ�˽�Ա�����¹���ˮƽ����1000λԱ���������ȡ100λԱ�����е��飬�õ����µ�Ƶ�ʷֲ�ֱ��ͼ�� 
��1�����ɴ�ͼ���Ƹù�˾Ա������ƽ�����ʣ�
��2���ù�˾���ʷ�������Ա����Ӫ��ˮƽΪ��Ҫ������ȷ���ģ�һ����Ϊ�����ʵ���4500Ԫ��Ա������ѧͽ�Σ�û��Ӫ�����飬������Ӫ������ʧ�ܣ�����4500Ԫ��Ա���Ǿ߱�Ӫ������Ա��������Ӫ������ɹ����ֽ����������ա�ѧͽ�ι��ʡ���������Ա�����ʡ���Ϊ���㣬���зֲ���������г��5�ˣ�����5������ѡ2�˽���Ӫ�������У�ÿλԱ����Ӫ���ɹ�����Ϊ��˾Ӯ��3��Ԫ������˾����ʧ1��Ԫ�������ڴ˴α����й�˾���������Ԫ�Ŀ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��= ![]() ��ax��eΪ��Ȼ�����ĵ��� ����������f��x����ͼ���ڵ㣨e2 �� f��e2�����������߷���Ϊ 3x+4y��e2=0����ʵ��a��b��ֵ��
��ax��eΪ��Ȼ�����ĵ��� ����������f��x����ͼ���ڵ㣨e2 �� f��e2�����������߷���Ϊ 3x+4y��e2=0����ʵ��a��b��ֵ��
����b=1ʱ�������� x1 �� x2��[e��e2]��ʹ f��x1����f�䣨x2��+a��������ʵ��a����Сֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com