练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，抛物线y＝ax2＋bx＋c（c≠0）过点（－1，0）和点（0，－2），且顶点在第四象限，设P＝a＋b＋c，则P的取值范是（ ）

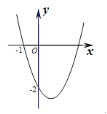
    A.－2＜P＜－1B.－2＜P＜0C.－4＜P＜0D.－4＜P＜－2

    【答案】C

    【解析】

    利用二次函数图象的开口方向和对称轴求出a>0，b<0，把点(1,0)和点(0,2)代入求出b=a-2，把x=1代入得出P=a+b+c=2a-4，求出2a-4的范围即可．

    ∵抛物线过点(1,0)和点(0,2).
    ∴0=ab+c，2=c，
    ∴b=a2，
    ∵当x=1时,y=ax2+bx+c=a+b+c，
    ∴P=a+b+c=a+a22=2a4，
    ∵顶点在第四象限，a>0，
    ∴b=a2<0，
    ∴a<2，
    ∴0<a<2，
    ∴4<2a4<0，
    即4<P<0.
    故选：C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】我区某中学为丰富学生的校园生活，准备从体育用品商店一次性购买若干个足球和篮球为关注儿童戍长的健康，实施“关注肥胖守儿童计划”，某校结全校各班肥胖儿童的人数情况进行了统计，发现各班留守儿童人数只有1名、2名、3名、4名、5名、6名共六种情况，并制成如下两幅不完整的统计图：

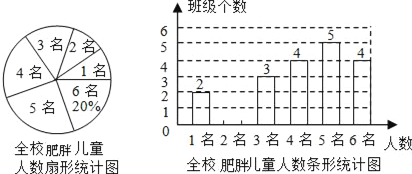
    （1）全校班级个数　 个　，并将该条形统计图补充完整；

    （2）为了了解肥胖儿重的饮食情况，某校决定从只有2名留守儿童的这些班级中，任选两名进行调查，请用列表法或画树形图的方法，求出所选两名肥胖儿童来自同一个班级的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

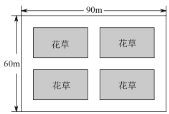
    【题目】成都市中心城区“小游园，微绿地”规划已经实施，武侯区某街道有一块矩形空地进入规划试点．如图，已知该矩形空地长为，宽为，按照规划将预留总面积为的四个小矩形区域（阴影部分）种植花草，并在花草周围修建三条横向通道和三条纵向通道，各通道的宽度相等．

    （1）求各通道的宽度；

    （2）现有一工程队承接了对这的区域（阴影部分）进行种植花草的绿化任务，该工程队先按照原计划进行施工，在完成了的绿化任务后，将工作效率提高，结果提前天完成任务，求该工程队原计划每天完成多少平方米的绿化任务？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】调查作业：了解你所住小区家庭3月份用气量情况

    小天、小东和小芸三位同学住在同一小区，该小区共有300户家庭，每户家庭人数在2～5之间，这300户家庭的平均人数约为3.3．

    小天、小东、小芸各自对该小区家庭3月份用气量情况进行了抽样裯查，将收集的数据进行了整理，绘制的统计表分别为表1、表2和表3．

    表1抽样调查小区4户家庭3月份用气量统计表（单位：m3）

    家庭人数

    2

    3

    4

    5

    用气量

    14

    19

    21

    26

    表2抽样调查小区15户家庭3月份用气量统计表（单位：m3）

    家庭人数

    2

    2

    2

    3

    3

    3

    3

    3

    3

    3

    3

    3

    3

    4

    用气量

    10

    11

    15

    13

    14

    15

    15

    17

    17

    18

    18

    18

    20

    22

    表3抽样调查小区15户家庭3月份用气量统计表（单位：m3）

    家庭人数

    2

    2

    2

    3

    3

    3

    3

    3

    3

    4

    4

    4

    4

    5

    5

    用气量

    10

    12

    13

    14

    17

    17

    18

    20

    20

    21

    22

    26

    31

    28

    31

    根据以|材料回答问题：

    （1）小天、小东和小芸三人中，哪位同学抽样调查的数据能较好地反映出该小区家庭3月份用气量情况？请简要说明其他两位同学抽样调查的不足之处．

    （2）在表3中，调查的15个家庭中使用气量的中位数是　 　m3，众数是　 　m3．

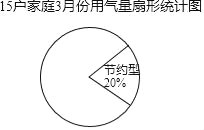
    （3）小东将表2中的数据按用气量x（m3）大小分为三类．

    ①节约型：10≤x≤13，②适中型：14≤x≤17，③偏高型：18≤x≤22，并绘制成如图扇形统讣图，请帮助他将扇形图补充完整．

    （4）小芸算出表3中3月份平均每人的用气量为6m3，请估计该小区3月份的总用气量．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，二次函数的图象与x轴的一个交点为A（3，0），另一个交点为B，且与y轴交于点C．

    （1）求m的值；

    （2）求点B的坐标；

    （3）该二次函数图像上有一点D（x，y）（其中，），使，求点D的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

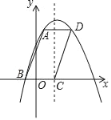
    【题目】如图，ABCD与抛物线y＝﹣x2+bx+c相交于点A，B，D，点C在抛物线的对称轴上，已知点B（﹣1，0），BC＝4．

    （1）求抛物线的解析式；

    （2）求BD的函数表达式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知矩形ABCD，P为BC上的一点，连接AP，过D点作DH⊥AP于H，AB=, BC=4,当△CDH为等腰三角形时，则BP=_________________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下列材料，解决材料后的问题：

    材料一：对于实数x、y，我们将x与y的“友好数”用f（x，y）表示，定义为：f（x）＝，例如17与16的友好数为f（17，16）＝＝．

    材料二：对于实数x，用[x]表示不超过实数x的最大整数，即满足条件[x]≤x＜[x]+1，例如：

    [﹣1.5]＝[﹣1.6]＝﹣2，[0]＝[0.7]＝0，[2.2]＝[2.7]＝2，……

    （1）由材料一知：x2+2与1的“友好数”可以用f（x2+2，1）表示，已知f（x2+2，1）＝2，请求出x的值；

    （2）已知[a﹣1]＝﹣3，请求出实数a的取值范围；

    （3）已知实数x、m满足条件x﹣2[x]＝，且m≥2x+，请求f（x，m2﹣m）的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】正方形中，是中点，点从点出发沿的路线匀速运动，到点停止，点从点出发，沿路线匀速运动，、两点同时出发，点的速度是点速度的倍，当点停止时，点也同时停止运动，设秒时，正方形与重叠部分的面积为，关于的函数关系如图2所示，则

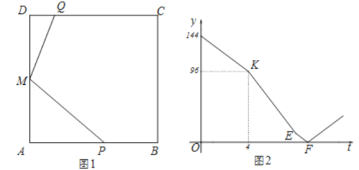
    （1）求正方形边长；

    （2）求的值；

    （3）求图2中线段所在直线的解析式.

    查看答案和解析>>

    同步练习册答案