
 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,矩形ABCO的边CO、OA分别在x轴、y轴上,点E在边BC上,将该矩形沿AE折叠,点B恰好落在边OC上的F处.若OA=8,CF=4,则点E的坐标是(-10,3).
如图,在平面直角坐标系中,矩形ABCO的边CO、OA分别在x轴、y轴上,点E在边BC上,将该矩形沿AE折叠,点B恰好落在边OC上的F处.若OA=8,CF=4,则点E的坐标是(-10,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在一次数学活动中,黑板上画着如图所示的图形,活动前老师在准备的四张卡片(大小、颜色、形状相同)的正面上分别写有如下四个等式中的一个等式:①AB=CD;②AD∥BC;③AB∥CD;④∠A=∠C;小英同学闭上眼睛从四张卡片中随机抽出一张,再从剩下的卡片中随机抽出另一张,请结合图形回答下列问题:
在一次数学活动中,黑板上画着如图所示的图形,活动前老师在准备的四张卡片(大小、颜色、形状相同)的正面上分别写有如下四个等式中的一个等式:①AB=CD;②AD∥BC;③AB∥CD;④∠A=∠C;小英同学闭上眼睛从四张卡片中随机抽出一张,再从剩下的卡片中随机抽出另一张,请结合图形回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
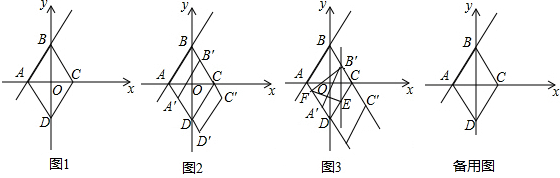
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com