
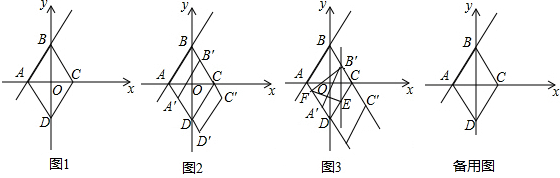
���� ��1��������εĶԽ��ߵij����ɽ�����⣮
��2���������жϡ�ABC����ACD�ǵȱ������Σ�����BB��=t�����Խ�����⣮
���г����̼��ɽ�����⣬ע���������Σ�
��3��������֤����EFB���ǵȱ������Σ���֤��EF��CD������DF=2DE�г����̼��ɽ�����⣮
����ͼ4�У����������ε�B1����BC��ʱ����B2����BC���ӳ�����ʱ�ֱ���⼴�ɣ�
��� �⣺��1����ͼ1�У�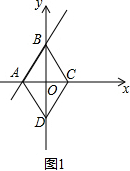
��ֱ��AB����ʽΪy=2x+3��
���A���꣨-$\frac{3}{2}$��0������B���꣨0��3����
��OA=$\frac{3}{2}$��OB=3��
���ı���ABCD�����Σ�
��AC=2OA=3��BD=6��
��S����ABCD=$\frac{1}{2}$•AC•BD=9��
�ʴ�Ϊ9��
��2����ͼ2�У�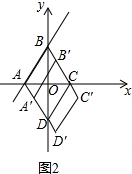
�١�ֱ��AB����ʽΪy=$\sqrt{3}$x+$\sqrt{3}$��
��A��-1��0����B��0��$\sqrt{3}$����
��OA=1��OB=$\sqrt{3}$��
��tan��BAO=$\frac{BO}{OA}$=$\sqrt{3}$��
���BAO=60�㣬
���ı���ABCD�����Σ�
���ABC����ACD���ǵȱ������Σ�
��BB��=t��
��B�䣨$\frac{1}{2}$t��$\sqrt{3}$-$\frac{\sqrt{3}}{2}$t��
�ʴ�Ϊ��$\frac{1}{2}$t��$\sqrt{3}$-$\frac{\sqrt{3}}{2}$t����
�ڵ�CB��=$\frac{1}{3}$BCʱ��������2-t=$\frac{1}{3}$��2��t-2=$\frac{1}{3}$��2��
���t=$\frac{4}{3}$��$\frac{8}{3}$��
��t=$\frac{4}{3}$��$\frac{8}{3}$��ʱCB��=$\frac{1}{3}$BC��
��3������ͼ3�У���CK��AD��K�����ı���CKFB���Ǿ��Σ�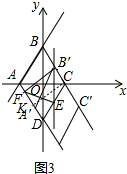
��B��E��BD��
���CB��E=��CBO=30�㣬
��B��F��AD��AD��BC��
��FB���CB��
���FB��C=90�㣬
���FB��E=60�㣬
�ߡ�EFB���ǵ��������Σ�
���EFB���ǵȱ������Σ�
���FEB��=60�㣬�ߡ�B��EC=30�㣬
���FEB��=90�㣬
��Rt��EFD�У��ߡ�EFD=30�㣬
��DF=2DE��
��2-t+1=2t��
��t=1��
��t=1ʱ����EFB���ǵ��������Σ�
����ͼ4�У�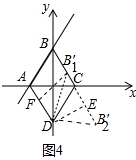
��B1����BC��ʱ���������֪DF=$\sqrt{2}$��
��2-t+1=$\sqrt{2}$��
��t=3-$\sqrt{2}$��
��B2����BC���ӳ�����ʱ��BB2��=3+$\sqrt{2}$��
��t=3+$\sqrt{2}$��
�൱t=��3$��\sqrt{2}$����ʱ���߶�B��D=$\sqrt{5}$��
���� ���⿼��һ�κ����ۺ��⡢���ε����ʣ�ֱ��������30�Ƚ����ʵ�֪ʶ������Ĺؼ���ѧ�������ת��Ϊ����ȥ˼����ѧ�����ӳ��ø����ߣ�����ֱ�������ν�����⣬�����п�ѹ���⣮


 ������״Ԫ���Ծ�ϵ�д�
������״Ԫ���Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x-y=1 | B�� | x=3 | C�� | x2-1=0 | D�� | 3y-1=0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ������ABCD�У�AD=5��AB=7����EΪDC��һ�����㣬�ѡ�ADE��AE�۵�����D�Ķ�Ӧ��ΪD�䣬��D�����ڡ�ABC��ƽ������ʱ��DE�ij�Ϊ��������
��ͼ������ABCD�У�AD=5��AB=7����EΪDC��һ�����㣬�ѡ�ADE��AE�۵�����D�Ķ�Ӧ��ΪD�䣬��D�����ڡ�ABC��ƽ������ʱ��DE�ij�Ϊ��������| A�� | 3��4 | B�� | $\frac{5}{2}$��$\frac{5}{3}$ | C�� | $\frac{5}{2}$��$\frac{3}{5}$ | D�� | $\frac{2}{5}$��$\frac{5}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
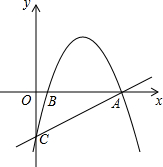 ��ͼ�������߾���A��4��0����B��1��0����C��0��-2�����㣮
��ͼ�������߾���A��4��0����B��1��0����C��0��-2�����㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com