
分析 先根据平方差公式求出A的值,根据21=2,22=4,23=8,24=16,25=32,26=64得出2128的末位数字是6,即可求出答案.
解答 解:A=(2+1)(22+1)(24+1)(28+1)(216+1)(232+1)(264+1),
=(2-1)(2+1)(22+1)(24+1)(28+1)(216+1)(232+1)(264+1),
=(24-1)(24+1)(28+1)(216+1)(232+1)(264+1),
=(28-1)(28+1)(216+1)(232+1)(264+1),
=(216-1)(216+1)(232+1)(264+1),
=(232-1)(232+1)(264+1)
=(264-1)(264+1)
=2128-1,
∵21=2,22=4,23=8,24=16,25=32,26=64,…,
∴128÷4=32,
∴2128的末位数字是6,
∴A-2002的末位数字是6-2=4,
故答案为:4
点评 本题考查了平方差公式的应用,解此题的关键是求出A=2128-1和得出2128的末位数字,注意:(a+b)(a-b)=a2-b2,题目比较好,难度适中.


科目:初中数学 来源: 题型:解答题
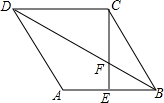 如图,四边形ABCD是菱形,CE⊥AB,垂足为点E,且CE交对角线BD于点F.若∠A=120°,四边形AEFD的面积为$\frac{5\sqrt{3}}{6}$,求EF的值.
如图,四边形ABCD是菱形,CE⊥AB,垂足为点E,且CE交对角线BD于点F.若∠A=120°,四边形AEFD的面积为$\frac{5\sqrt{3}}{6}$,求EF的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
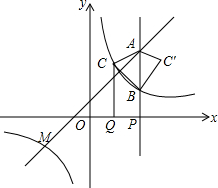 如图,点M(-3,m)是一次函数y=x+1与反比例函数y=$\frac{k}{x}$(k≠0)的图象的一个交点.
如图,点M(-3,m)是一次函数y=x+1与反比例函数y=$\frac{k}{x}$(k≠0)的图象的一个交点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com