
【题目】己知:![]() 、
、![]() 都是关于
都是关于![]() 的多项式,
的多项式,![]() ,
,![]() ,其中多项式
,其中多项式![]() 有一项被“□”遮挡住了.
有一项被“□”遮挡住了.
(1)当![]() 时,
时,![]() ,请求出多项式
,请求出多项式![]() 被“□”遮挡的这一项的系数;
被“□”遮挡的这一项的系数;
(2)若![]() 是单项式,请直接写出多项式
是单项式,请直接写出多项式![]() .
.
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】A,B两地之间有一条6000米长的直线跑道,小月和小华分别从A,B两地同时出发匀速跑步,相向而行,第一次相遇后,小月将自己的速度提高25%,并匀速跑步到达B点,到达后原地休息;小华匀速跑步到达A点后,立即调头按原速返回B点(调头时间忽略不计),两人距各自出发点的距离之和记为y(米),跑步时间记为x(分钟),已知y(米)与x(分钟)之间的关系如图所示,则小月到达B点后,再经过_____分钟小华回到B点.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文化源远流长,文学方面,《西游记》、《三国演义》、《水浒传》、《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”某中学为了解学生对四大名著的阅读情况,就“四大古典名著你读完了几部”的问题在全校学生中进行了抽样调查,根据调查结果绘制成如下尚不完整的统计图.
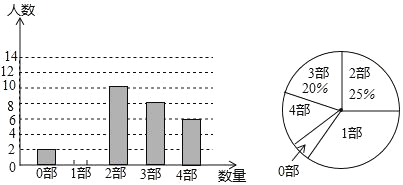
请根据以上信息,解决下列问题
(1)本次调查所得数据的众数是____部,中位数是_____部;
(2)扇形统计图中“4部”所在扇形的圆心角为_____度;
(3)请将条形统计图补充完整;
(4)没有读过四大古典名著的两名学生准备从中各自随机选择一部来阅读,求他们恰好选中同一名著的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A、C、F在坐标轴上,E是OA的中点,四边形AOCB是矩形,四边形BDEF是正方形,若点C的坐标为(3,0),则点D的坐标为( )
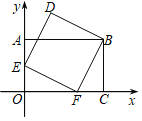
A. (1,2.5)B. (1,1+ ![]() )C. (1,3)D. (
)C. (1,3)D. (![]() ﹣1,1+
﹣1,1+ ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
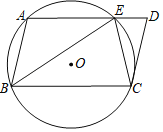
【题目】如图,在ABCD中,过A、B、C三点的⊙O交AD于点E,连接BE、CE,BE=BC.
(1)求证:△BEC∽△CED;
(2)若BC=10,DE=3.6,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
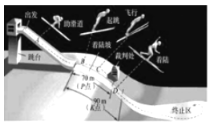
【题目】跳台滑雪是冬季奥运会比赛项目之一,如图平面直角坐标系是跳台滑雪的截面示意图,运动员沿滑道![]() 下滑,在
下滑,在![]() 轴上的点
轴上的点![]() 起跳,点
起跳,点![]() 距落地水平面
距落地水平面![]() 轴
轴![]() ,运动员落地的雪面开始是一段曲线
,运动员落地的雪面开始是一段曲线![]() ,到达点
,到达点![]() 后变为水平面,点
后变为水平面,点![]() 距
距![]() 轴的水平距离为
轴的水平距离为![]() .运动员(看成点)从点
.运动员(看成点)从点![]() 起跳后的水平速度为
起跳后的水平速度为![]() ,点
,点![]() 是下落路线的某位置.忽略空气阻力,实验表明:
是下落路线的某位置.忽略空气阻力,实验表明:![]() ,
,![]() 的竖直距离
的竖直距离![]() 与飞出时间
与飞出时间![]() 的平方成正比,且
的平方成正比,且![]() 时
时![]() ;
;![]() ,
,![]() 的水平距离是
的水平距离是![]() 米.
米.
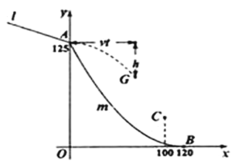
(1)用含![]() 的代数式表示
的代数式表示![]() ;
;
(2)用含![]() 、
、![]() 的代数式表示点
的代数式表示点![]() 的横坐标
的横坐标![]() 和纵坐标
和纵坐标![]() ,并求
,并求![]() 与
与![]() 的关系式(不写
的关系式(不写![]() 的取值范围);
的取值范围);
(3)奥运组委会规定,运动员落地点距起跳点的水平距离为运动员本次跳跃的成绩,并且参赛的达标成绩为![]() .在运动员跳跃的过程中,点
.在运动员跳跃的过程中,点![]() 处有一个摄像头,记录运动员的空中姿态,当运动员飞过点
处有一个摄像头,记录运动员的空中姿态,当运动员飞过点![]() 时,在点
时,在点![]() 上方可被摄像头抓拍到.若运动员本次跳跃达到达标成绩,并且能被
上方可被摄像头抓拍到.若运动员本次跳跃达到达标成绩,并且能被![]() 处摄像头抓拍,求从点
处摄像头抓拍,求从点![]() 起跳后的水平速度
起跳后的水平速度![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 ;
(2)将条形统计图补充完整.观察此图,支付方式的“众数”是“ ”;
(3)在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,新生活超市在端午节前夕购进价格为3元/个的某品牌粽子,根据市场预测,该品牌粽子每个售价4元时,每天能出售500个,并且售价每上涨0.1元,其销售量将减少10个,为了维护消费者利益,物价部门规定,该品牌粽子售价不能超过进价的200%,请你利用所学知识帮助超市给该品牌粽子定价,使超市每天的销售利润为800元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,经过原点O的抛物线![]() (a≠0)与x轴交于另一点A(
(a≠0)与x轴交于另一点A(![]() ,0),在第一象限内与直线y=x交于点B(2,t).
,0),在第一象限内与直线y=x交于点B(2,t).
(1)求这条抛物线的表达式;
(2)在第四象限内的抛物线上有一点C,满足以B,O,C为顶点的三角形的面积为2,求点C的坐标;
(3)如图2,若点M在这条抛物线上,且∠MBO=∠ABO,在(2)的条件下,是否存在点P,使得△POC∽△MOB?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com