
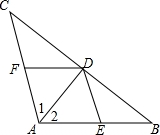
 如图,AD是△ABC的角平分线,DE∥AC交AB于点E,DF∥AB 交AC于F.试判断四边形AEDF是怎样的四边形?并说明理由.
如图,AD是△ABC的角平分线,DE∥AC交AB于点E,DF∥AB 交AC于F.试判断四边形AEDF是怎样的四边形?并说明理由.  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
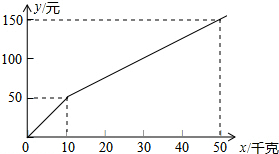 某种子公司以一定价格销售“黄金1号”玉米种子,如果一次购买10千克以上(不含10千克)的种子,超过10千克的那部分种子的价格打折,因此付款金额y(单位:元)与一次购买种子数量x(单位:千克)之间的函数关系如果所示,下列四种说法:
某种子公司以一定价格销售“黄金1号”玉米种子,如果一次购买10千克以上(不含10千克)的种子,超过10千克的那部分种子的价格打折,因此付款金额y(单位:元)与一次购买种子数量x(单位:千克)之间的函数关系如果所示,下列四种说法:| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{13}{7}$ | B. | $\frac{20}{7}$ | C. | $\frac{27}{7}$ | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com