
【题目】如图,平行四边形![]() 中,
中,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() ,且
,且![]() ,延长
,延长![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() ,
,![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() 是等边三角形;③
是等边三角形;③![]() ;④
;④![]() ;⑤
;⑤![]() 中正确的有( )
中正确的有( )

A.1个B.2个C.3个D.4个
【答案】C
【解析】
由平行四边形的性质得出AD∥BC,AD=BC,由AE平分∠BAD,可得∠BAE=∠DAE,可得∠BAE=∠BEA,得AB=BE,由AB=AE,得到△ABE是等边三角形,②正确;则∠ABE=∠EAD=60°,由SAS证明△ABC≌△EAD,①正确;由△FCD与△ABD等底(AB=CD)等高(AB与CD间的距离相等),得出S△FCD=S△ABD,由△AEC与△DEC同底等高,所以S△AEC=S△DEC,得出S△ABE=S△CEF,⑤正确.
解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠EAD=∠AEB,
又∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠BEA,
∴AB=BE,
∵AB=AE,
∴△ABE是等边三角形;
②正确;
∴∠ABE=∠EAD=60°,
∵AB=AE,BC=AD,
在△ABC和△EAD中,
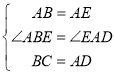 ,
,
∴△ABC≌△EAD(SAS);
①正确;
∵△FCD与△ABC等底(AB=CD)等高(AB与CD间的距离相等),
∴S△FCD=S△ABC,
又∵△AEC与△DEC同底等高,
∴S△AEC=S△DEC,
∴S△ABE=S△CEF;
⑤正确;
若AD与AF相等,即∠AFD=∠ADF=∠DEC,
即EC=CD=BE,
即BC=2CD,
题中未限定这一条件,
∴③④不一定正确;
故选C.


科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,给出四个结论:
①c>0;
②若点B(﹣ ![]() ,y1)、C(﹣
,y1)、C(﹣ ![]() ,y2)为函数图象上的两点,则y1<y2;
,y2)为函数图象上的两点,则y1<y2;
③2a﹣b=0;
④ ![]() <0,
<0,
其中,正确结论的个数是( )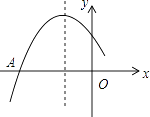
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:把形如![]() 的二次三项式(或其一部分)配成完全平方式的方法叫做配方法.配方法的基本形式是完全平方公式的逆写,即
的二次三项式(或其一部分)配成完全平方式的方法叫做配方法.配方法的基本形式是完全平方公式的逆写,即![]() .例如:
.例如:![]()
![]() 是
是![]() 的一种形式的配方;所以,
的一种形式的配方;所以,![]() ,
,![]()
![]() ,
,![]() 是
是![]() 的三种不同形式的配方(即“余项”分别是常数项、一次项、二次项).
的三种不同形式的配方(即“余项”分别是常数项、一次项、二次项).
请根据阅读材料解决下列问题:
(1)比照上面的例子,写出![]() 三种不同形式的配方;
三种不同形式的配方;
(2)已知![]() ,求
,求![]() 的值;
的值;
(3)已知![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC=6,∠ACB>90°,∠ABC的平分线交AC于点D,E是AB上一点,且BE=BC,CF∥ED交BD于点F,连接EF,ED.
(1)求证:四边形CDEF是菱形.
(2)当∠ACB= 度时,四边形CDEF是正方形,请给予证明;并求此时正方形的边长。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人到一家快递公司办理环江香米(简称香米)的快递托运,重量为![]() 千克.快递公司收取托运费方案如下:
千克.快递公司收取托运费方案如下:
凡物品重量不超过10千克的,按2元/千克收取托运费;当物品重量超过10千克的,超出部分按3元/千克加收托运费.
(1)写出![]() 千克香米的托运费的表达式 (用含字母
千克香米的托运费的表达式 (用含字母![]() 的式子表示);
的式子表示);
(2)若托运香米重量为![]() 千克时,求出这笔托运费.
千克时,求出这笔托运费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有个填写运算符号的游戏:在“ 1□3□9□7” 中的每个□内,填入![]() ,
,![]() ,
,![]() ,
,![]() 中的某一个(可重复使用),然后计算结果.
中的某一个(可重复使用),然后计算结果.
(1)计算:![]() ;
;
(2)若1![]() 3×9□7= -4,请推算□内的符号;
3×9□7= -4,请推算□内的符号;
(3)在“1□3□9-7”的□内填入符号后,使计算所得数最小,直接写出这个最小数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教育部明确要求中小学生每天要有2小时体育锻炼,周末朱诺和哥哥在![]() 米的环形跑道上骑车锻炼,他们在同一地点沿着同一方向同时出发,骑行结束后两人有如下对话:
米的环形跑道上骑车锻炼,他们在同一地点沿着同一方向同时出发,骑行结束后两人有如下对话:
朱诺:你要![]() 分钟才能第一次追上我.
分钟才能第一次追上我.
哥哥:我骑完一圈的时候,你才骑了半圈!
(1)请根据他们的对话内容,求出朱诺和哥哥的骑行速度(速度单位:米/秒);
(2)哥哥第一次追上朱诺后,在第二次相遇前,再经过多少秒,朱诺和哥哥相距![]() 米?
米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知一次函数y=ax+2与x轴、y轴分别交于点A,B,反比例函数y= ![]() 经过点M.
经过点M.
(1)若M是线段AB上的一个动点(不与点A、B重合).当a=﹣3时,设点M的横坐标为m,求k与m之间的函数关系式.
(2)当一次函数y=ax+2的图象与反比例函数y= ![]() 的图象有唯一公共点M,且OM=
的图象有唯一公共点M,且OM= ![]() ,求a的值.
,求a的值.
(3)当a=﹣2时,将Rt△AOB在第一象限内沿直线y=x平移 ![]() 个单位长度得到Rt△A′O′B′,如图2,M是Rt△A′O′B′斜边上的一个动点,求k的取值范围.
个单位长度得到Rt△A′O′B′,如图2,M是Rt△A′O′B′斜边上的一个动点,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你能求(x一1)(x99+x98+x97+…+x+1)的值吗?
遇到这样的问题,我们可以先思考一下,从简单的情形人手,分别计算下列各式的值.
(1)(x-1)(x+1) =_____________;
(2)(x—1)( x2+x+1) =_____________;
(3)(x-1)(x3+ x2+x+1) =____________;
…
由此我们可以得到:
(4)(x一1)( x99+x98+x97+…+x+1) =___________,
请你利用上面的结论,完成下列的计算:
(5)299+298+297+…+2+1;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com