Question

【题目】已知：如图所示，在△ABC中，∠B=90°，AB=5cm，BC=7cm，点P从点A开始沿AB边向点B以1cm/s的速度移动，点Q从点B开始沿BC边向点C以2cm/s的速度移动．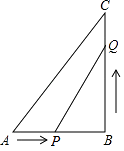
（1）如果P，Q分别从A，B同时出发，那么几秒后，△PBQ的面积等于4cm2？
（2）如果P，Q分别从A，B同时出发，那么几秒后，PQ的长度等于2 cm？
（3）在（1）中，△PQB的面积能否等于7cm2？说明理由．

Answer 1

【答案】
（1）解：设经过x秒以后△PBQ面积为4cm2，根据题意得 （5﹣x）×2x=4，

整理得：x2﹣5x+4=0，

解得：x=1或x=4（舍去）．

答：1秒后△PBQ的面积等于4cm2

（2）解：PQ=2 ，则PQ2=25=BP2+BQ2，即40=（5﹣t）2+（2t）2，

解得：t=0（舍去）或3．

则3秒后，PQ的长度为2 cm

（3）解：令S△PQB=7，即BP× =7，（5﹣t）× =7，

整理得：t2﹣5t+7=0，

由于b2﹣4ac=25﹣28=﹣3＜0，

则原方程没有实数根，

所以在（1）中，△PQB的面积不能等于7cm2

【解析】（1）经过x秒钟，△PBQ的面积等于4cm2 ， 根据点P从A点开始沿AB边向点B以1cm/s的速度移动，点Q从B点开始沿BC边向点C以2cm/s的速度移动，表示出BP和BQ的长可列方程求解；（2）利用勾股定理列出方程求解即可；（3）令S△PQB=7，根据三角形的面积公式列出方程，再根据b2﹣4ac得出原方程没有实数根，从而得出△PQB的面积不能等于7cm2 ．
【考点精析】掌握勾股定理的概念是解答本题的根本，需要知道直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2．