
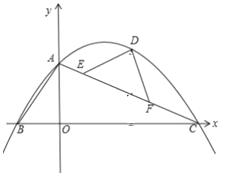
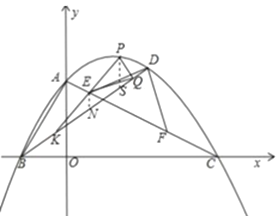
【题目】如图,平面直角坐标系中,O为坐标原点,直线y=﹣![]() x+4交x轴于点C,交y轴于点A,过A、C两点的抛物线y=ax2+bx+4交x轴负半轴于点B,且tan∠BAO=
x+4交x轴于点C,交y轴于点A,过A、C两点的抛物线y=ax2+bx+4交x轴负半轴于点B,且tan∠BAO=![]() .
.
(1)求抛物线的解析式;
(2)已知E、F是线段AC上异于A、C的两个点,且AE<AF,EF=2![]() ,D为抛物线上第一象限内一点,且DE=DF,设点D的横坐标为m,△DEF的面积为S,求S与m的函数关系式(不要求写出自变量m的取值范围);
,D为抛物线上第一象限内一点,且DE=DF,设点D的横坐标为m,△DEF的面积为S,求S与m的函数关系式(不要求写出自变量m的取值范围);
(3)在(2)的条件下,当∠EDF=90°时,连接BD,P为抛物线上一动点,过P作PQ⊥BD交线段BD于点Q,连接EQ.设点P的横坐标为t,求t为何值时,PE=QE.
【答案】(1)y=﹣![]() x2+
x2+![]() x+4;(2)S=﹣
x+4;(2)S=﹣![]() m2+
m2+![]() m;(3)当t的值为1+
m;(3)当t的值为1+![]() 或1﹣
或1﹣![]() 时,PE=QE.
时,PE=QE.
【解析】
(1)令﹣![]() x+4=0,解得x=8,令x=0,y=4,由tan∠BAO=
x+4=0,解得x=8,令x=0,y=4,由tan∠BAO=![]() ,OA=4,得OB=3,由以上可得点A、B、C坐标,然后利用待定系数法进行求解即可;
,OA=4,得OB=3,由以上可得点A、B、C坐标,然后利用待定系数法进行求解即可;
(2)点坐标转换为线段长度,再利用相似三角形找到线段间的比例关系,继而可求出S与m的函数关系式;
(3)可利用(2)得到线段的长度,再综合分析(3)给出的已知信息,可知△EDF为等腰直角三角形,从而得到点E、D的坐标,继而结合三角形中位线定理等知识列式求解即可.
(1)令﹣![]() x+4=0,解得x=8,∴C(8,0),
x+4=0,解得x=8,∴C(8,0),
令x=0,y=4,∴A(0,4),AC=4![]() ,
,
∵tan∠BAO=![]() ,OA=4,∴OB=3,
,OA=4,∴OB=3,
∴B(﹣3,0),
将点B、C代入抛物线y=ax2+bx+4得,
![]() ,
,
解得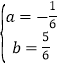 ,
,
∴抛物线得解析式为y=﹣![]() x2+
x2+![]() x+4;
x+4;
(2)如图所示,过点D作x轴的垂线,垂足为G,交AC于点K,过点D作EF的垂线,垂足为H,
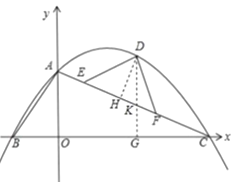
∵点D的横坐标为m,当x=m时,
y=﹣![]() m2+
m2+![]() m+4,
m+4,
设直线AC的解析式为y=kx+b,代入点A、C,
![]() ,
,
解得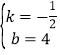 ,
,
∴y=﹣![]() x+4,
x+4,
∴K(m,﹣![]() m+4),
m+4),
∴DK=﹣![]() m2+
m2+![]() m+4﹣(﹣
m+4﹣(﹣![]() m+4)=﹣
m+4)=﹣![]() m2+
m2+![]() m,
m,
∵△DHK∽△COA,
∴![]() ,
,
∴![]() ,
,
∴DH=![]() (﹣
(﹣![]() m2+
m2+![]() m),
m),
∴S=![]() EFDH=﹣
EFDH=﹣![]() m2+
m2+![]() m;
m;
(3)由(2)可知,DH=![]() (﹣
(﹣![]() m2+
m2+![]() m),
m),
∵EF=2![]() ,DE=DF,且∠EDF=90°,
,DE=DF,且∠EDF=90°,
∴DH=![]() ,
,
∴![]() =
=![]() (﹣
(﹣![]() m2+
m2+![]() m),
m),
解得m1=3,m2=5,
当m=3时,点E与点A重合,不符合题意舍,
∴m=5,
∴D(5,4),
设点E的坐标为(k,﹣![]() k+4),DE=
k+4),DE=![]() EF=
EF=![]() ,
,
DE=![]() =
=![]() ,
,
解得k1=2,k2=6,
∵E在点D左侧,∴k=2,
∴E(2,3),
连接BD,设BD的解析式为y=kx+b,代入点B、D,
![]() ,解得
,解得![]() ,
,
∴直线BD的解析式为y=![]() x+
x+![]() ,
,
过点E作y轴的平行线交BD于点N,
则点N的坐标为(2,![]() ),
),
∴EN=![]() ,
,
连接PE并延长交BD于点K,
∵∠PQK=90°,EP=EQ,
∴∠EPQ=∠EQP,
∴∠EKQ=∠EQK,
∴EQ=EK=EP,
∴点E为PK的中点,
过点P作y轴的平行线交BD于点S,
∴PS=2EN,
∵P(t,-![]() t2+
t2+![]() t+4),
t+4),
∴S(t,![]() t+
t+![]() ),
),
∴PS=-![]() t2+
t2+![]() t+
t+![]() ,
,
∴-![]() t2+
t2+![]() t+
t+![]() =1,
=1,
解得t1=1+![]() ,t2=1﹣
,t2=1﹣![]() ,
,
∴当t的值为1+![]() 或1﹣
或1﹣![]() 时,PE=QE.
时,PE=QE.


科目:初中数学 来源: 题型:
【题目】如图,已知![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上,以
上,以![]() 为圆心,
为圆心,![]() 为半径的弧经过点
为半径的弧经过点![]() 是弧
是弧![]() 上一个动点.
上一个动点.
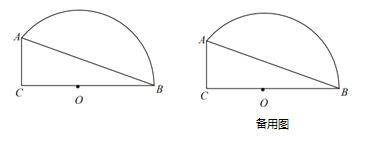
![]() 求半径
求半径![]() 的长;
的长;
![]() 如果点
如果点![]() 是弧
是弧![]() 的中点,联结
的中点,联结![]() ,求
,求![]() 的正切值;
的正切值;
![]() 如果
如果![]() 平分
平分![]() ,延长
,延长![]() 交于点
交于点![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知梯形ABCD中,AD∥BC,AB=AC,E是边BC上的点,且∠AED=∠CAD,DE交AC于点F.
(1)求证:△ABE∽△DAF;
(2)当ACFC=AEEC时,求证:AD=BE.

查看答案和解析>>
科目:初中数学 来源: 题型:
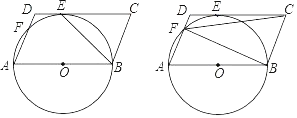
【题目】如图,四边形ABCD是平行四边形,以AB为直径的⊙O与CD切于点E,AD交⊙O于点F.
(1)求证:∠ABE=45°;
(2)连接CF,若CE=2DE,求tan∠DFC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家为了实现2020年全面脱贫目标,实施“精准扶贫”战略,采取异地搬迁,产业扶持等措施.使贫困户的生活条件得到改善,生活质量明显提高.某旗县为了全面了解贫困县对扶贫工作的满意度情况,进行随机抽样调查,分为四个类别:A.非常满意;B.满意;C.基本满意;D.不满意.依据调查数据绘制成图1和图2的统计图(不完整).
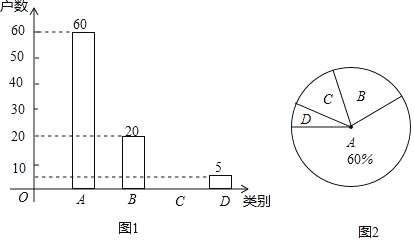
根据以上信息,解答下列问题:
(1)将图1补充完整;
(2)通过分析,贫困户对扶贫工作的满意度(A、B、C类视为满意)是 ;
(3)市扶贫办从该旗县甲乡镇3户、乙乡镇2户共5户贫困户中,随机抽取两户进行满意度回访,求这两户贫困户恰好都是同一乡镇的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)“切实减轻学生课业负担”是我市作业改革的一项重要举措.某中学为了解本校学生平均每天的课外作业时间,随机抽取部分学生进行问卷调查,并将调查结果分为A、B、C、D四个等级.A:1小时以内,B:1小时-1.5小时,C:1.5小时-2小时,D:小时以上.根据调查结果绘制了如图所示的两幅不完整的统计图.请根据图中信息解答下列问题:
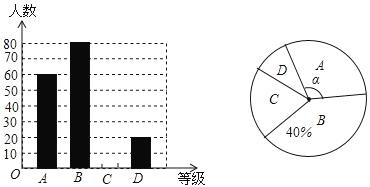
(1)该校共调查了_________名学生;
(2)请将条形统计图补充完整;
(3)表示等级A的扇形圆心角![]() 的度数是____________;
的度数是____________;
(4)在此次问卷调查中,甲、乙两班各有2人平均每天课外作业时间都是2小时以上,从这4人中任选2人去参加座谈,用列表或树状图的方法求选出的2人来自不同班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,BA=BC.点D是AB的中点,连结CD,过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连结DF.给出以下四个结论:①![]() ;②点F是GE的中点;③AF=
;②点F是GE的中点;③AF=![]() AB;④S△ABC=5S△BDF,其中正确的结论序号是( )
AB;④S△ABC=5S△BDF,其中正确的结论序号是( )
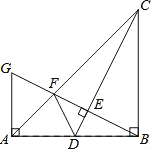
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣x+b与双曲线![]() 交于A、B两点,连接OA、OB,AM⊥y轴于点M,BN⊥x轴于点N,有以下结论:①S△AOM=S△BON;②OA=OB;③五边形MABNO的面积
交于A、B两点,连接OA、OB,AM⊥y轴于点M,BN⊥x轴于点N,有以下结论:①S△AOM=S△BON;②OA=OB;③五边形MABNO的面积![]() ;④若∠AOB=45°,则S△AOB=2k,⑤当AB=
;④若∠AOB=45°,则S△AOB=2k,⑤当AB=![]() 时,ON﹣BN=1;其中结论正确的个数有( )
时,ON﹣BN=1;其中结论正确的个数有( )
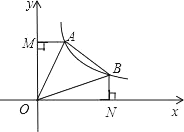
A. 5个B. 4个C. 3个D. 2个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com