
【题目】已知:等边![]() 分别是
分别是![]() 上的动点,且
上的动点,且![]() ,
,![]() 交于点
交于点![]() .
.
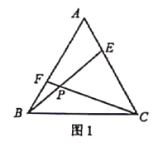
![]() 如图1,当点
如图1,当点![]() 分别在线段
分别在线段![]() 和线段
和线段![]() 上时,求
上时,求![]() 的度数;
的度数;
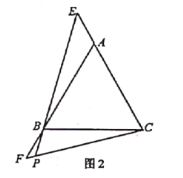
![]() 如图2,当点
如图2,当点![]() 分别在线段
分别在线段![]() 和线段
和线段![]() 的延长线上时,求
的延长线上时,求![]() 的度数.
的度数.
【答案】(1)∠CPE=60°;(2)60°
【解析】
![]() 根据等边三角形性质得出∠BAC=∠ABC=∠ACB=60°,AB=AC,根据SAS证△AFC≌△CEB,推出∠ACF=∠CBE,根据三角形的外角性质求出即可;
根据等边三角形性质得出∠BAC=∠ABC=∠ACB=60°,AB=AC,根据SAS证△AFC≌△CEB,推出∠ACF=∠CBE,根据三角形的外角性质求出即可;
![]() 同理证明△AFC≌△CEB,推出∠F=∠E,根据三角形的外角性质求出即可.
同理证明△AFC≌△CEB,推出∠F=∠E,根据三角形的外角性质求出即可.
(1)∵△ABC是等边三角形,
∴∠BAC=∠ABC=∠ACB=60°,AB=AC,
∵在AFC和△CEB中
 ,
,
∴AFC≌△CEB(SAS),
∴∠ACF=∠CBE,
∴![]() =∠CBE+∠BCF
=∠CBE+∠BCF
=∠ACF +∠BCF
=∠ACB
=60°;
(2)同理在AFC和△CEB中
 ,
,
∴AFC≌△CEB(SAS),
∴∠F=∠E,,
∴![]() =∠FBP+∠F
=∠FBP+∠F
=∠EBA +∠E
=∠BAC
=60°.


科目:初中数学 来源: 题型:
【题目】如图,以直线AB上一点O为端点作射线OC,使∠AOC=65°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
(1)如图①,若直角三角板DOE的一边OD放在射线OA上,则∠COE= ;
(2)如图②,将直角三角板DOE绕点O顺时针方向转动到某个位置,若OC恰好平分∠AOE,求∠COD的度数;
(3)如图③,将直角三角板DOE绕点O任意转动,如果OD始终在∠AOC的内部,试猜想∠AOD和∠COE有怎样的数量关系?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电子厂商投产一种新型电子产品,每件制造成本为18元,试销过程中发现,每月销售量![]() (万件)与销售单价
(万件)与销售单价![]() (元)之间的关系可以近似地看作一次函数
(元)之间的关系可以近似地看作一次函数![]() .(利润=售价-制造成本)
.(利润=售价-制造成本)
(1)写出每月的利润![]() (万元)与销售单价
(万元)与销售单价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)当销售单价为多少元时,厂商每月获得的利润为440万元?
(3)根据相关部门规定,这种电子产品的销售单价不能高于40元,如果厂商每月的制造成本不超过540万元,那么当销售单价为多少元时,厂商每月获得的利润最大?最大利润为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知长方形ABCD中,AD=6cm,AB=4cm,点E为AD的中点.若点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BC上由点B向点C运动.
(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△AEP与△BPQ是否全等,请说明理由,并判断此时线段PE和线段PQ的位置关系;
(2)若点Q的运动速度与点P的运动速度相等,运动时间为t秒,设△PEQ的面积为Scm2,请用t的代数式表示S;
(3)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△AEP与△BPQ全等?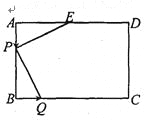
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E为BC边上一点,连接AE,作AE的垂直平分线交AB于G,交CD于F.若DF=2,BG=4,则GF的长为___________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线上![]() ,它与
,它与![]() 轴交于
轴交于![]() ,与
,与![]() 轴交于
轴交于![]() 、
、![]() ,
,![]() 是抛物线上
是抛物线上![]() 、
、![]() 之间的一点,
之间的一点,
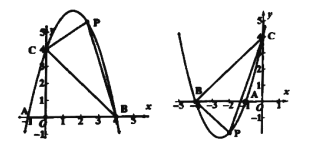
(1)当![]() 时,求抛物线的方程,并求出当
时,求抛物线的方程,并求出当![]() 面积最大时的
面积最大时的![]() 的横坐标。
的横坐标。
(2)当![]() 时,求抛物线的方程及
时,求抛物线的方程及![]() 的坐标,并求当
的坐标,并求当![]() 面积最大时
面积最大时![]() 的横坐标。
的横坐标。
(3)根据(1)、(2)推断![]() 的横坐标与
的横坐标与![]() 的横坐标有何关系?
的横坐标有何关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是圆上一点,弦CD⊥AB于点E,且DC=AD.过点A作⊙O的切线,过点C作DA的平行线,两直线交于点F,FC的延长线交AB的延长线于点G.
(1)求证:FG与⊙O相切;
(2)连接EF,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店销售单价分别为![]() 元/筒、
元/筒、![]() 元/筒的甲、乙两种羽毛球.根据消费者需求,该网店决定用不超过
元/筒的甲、乙两种羽毛球.根据消费者需求,该网店决定用不超过![]() 元购进甲、乙两种羽毛球共
元购进甲、乙两种羽毛球共![]() 简.且甲种羽毛球的数量大于乙种羽毛球数量的
简.且甲种羽毛球的数量大于乙种羽毛球数量的![]() .已知甲、乙两种羽毛球的进价分别为
.已知甲、乙两种羽毛球的进价分别为![]() 元/筒、
元/筒、![]() 元/筒。若设购进甲种羽毛球
元/筒。若设购进甲种羽毛球![]() 简.
简.
(1)该网店共有几种进货方案?
(2)若所购进羽毛球均可全部售出,求该网店所获利润![]() (元)与甲种羽毛球进货量
(元)与甲种羽毛球进货量![]() (简)之间的函数关系式,并求利润的最大值
(简)之间的函数关系式,并求利润的最大值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com