
【题目】某网店销售单价分别为![]() 元/筒、
元/筒、![]() 元/筒的甲、乙两种羽毛球.根据消费者需求,该网店决定用不超过
元/筒的甲、乙两种羽毛球.根据消费者需求,该网店决定用不超过![]() 元购进甲、乙两种羽毛球共
元购进甲、乙两种羽毛球共![]() 简.且甲种羽毛球的数量大于乙种羽毛球数量的
简.且甲种羽毛球的数量大于乙种羽毛球数量的![]() .已知甲、乙两种羽毛球的进价分别为
.已知甲、乙两种羽毛球的进价分别为![]() 元/筒、
元/筒、![]() 元/筒。若设购进甲种羽毛球
元/筒。若设购进甲种羽毛球![]() 简.
简.
(1)该网店共有几种进货方案?
(2)若所购进羽毛球均可全部售出,求该网店所获利润![]() (元)与甲种羽毛球进货量
(元)与甲种羽毛球进货量![]() (简)之间的函数关系式,并求利润的最大值
(简)之间的函数关系式,并求利润的最大值
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,某地方政府决定在相距50km的A、B两站之间的公路旁E点,修建一个土特产加工基地,且使C、D两村到E点的距离相等,已知DA⊥AB于A,CB⊥AB于B,DA=30km,CB=20km,那么基地E应建在离A站多少千米的地方?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点O在直线AB上,作射线OC,点D在平面内,∠BOD与∠AOC互余.
(1)若∠AOC:∠BOD=4:5,则∠BOD= ;
(2)若∠AOC=α(0°<α≤45°),ON平分∠COD.
①当点D在∠BOC内,补全图形,直接写出∠AON的值(用含α的式子表示);
②若∠AON与∠COD互补,求出α的值.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现将三张形状、大小完全相同的平行四边形透明纸片分别放在方格纸中,方格纸中的每个小正方形的边长均为1,并且平行四边形 纸片的每个顶点与小正方形的顶点重合(如图①、图②、图③).


图②矩形(正方形)
 ,
,
分别在图①、图②、图③中,经过平行四边形纸片的任意一个顶点画一条裁剪线,沿此裁剪线将平行四边形纸片裁成两部分,并把这两部分重新拼成符合下列要求的几何图形.
要求:
(1)在左边的平行四边形纸片中画一条裁剪线,然后在右边相对应的方格纸中,按实际大小画出所拼成的符合要求的几何图形.
(2)裁成的两部分在拼成几何图形时要互不重叠且不留空隙.
(3)所画出的几何图形的各顶点必须与小正方形的顶点重合.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知正方形ABCD,E是线段BC上一点,N是线段BC延长线上一点,以AE为边在直线BC的上方作正方形AEFG.

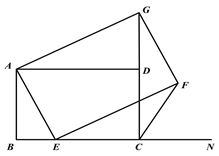
图(1) 图(2)
(1)连接GD,求证:DG=BE;
(2)连接FC,求∠FCN的度数;
(3)如图(2),将图(1)中正方形ABCD改为矩形ABCD,AB=m,BC=n(m、n为常数),E是线段BC上一动点(不含端点B、C),以AE为边在直线BC的上方作矩形AEFG,使顶点G恰好落在射线CD上.判断当点E由B向C运动时,∠FCN的大小是否总保持不变?若∠FCN的大小不变,请用含m、n的代数式表示tan∠FCN的值;若∠FCN的大小发生改变,请画图说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、丙两地相距500km,一列快车从甲地驶往丙地,途中经过乙地;一列慢车从乙地驶往丙地,两车同时出发,同向而行,折线ABCD表示两车之间的距离y(km)与慢车行驶的时间为x(h)之间的函数关系.根据图中提供的信息,下列说法不正确的是( )
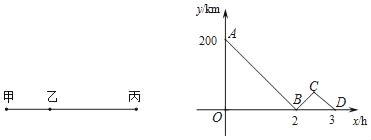
A. 甲、乙两地之间的距离为200 kmB. 快车从甲地驶到丙地共用了2.5 h
C. 快车速度是慢车速度的1.5倍D. 快车到达丙地时,慢车距丙地还有50 km
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求画图:(1)如图1平面上有五个点![]() ,按下列要求画出图形.
,按下列要求画出图形.
①连接![]() ;
;
②画直线![]() 交
交![]() 于点
于点![]() ;
;
③画出线段![]() 的反向延长线;
的反向延长线;
④请在直线![]() 上确定一点
上确定一点![]() ,使
,使![]() 两点到点
两点到点![]() 的距离之和最小,并写出画图的依据.
的距离之和最小,并写出画图的依据.
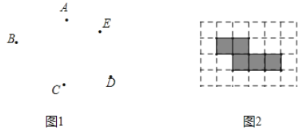
(2)有5个大小一样的正方形制成如图2所示的拼接图形(阴影部分),请你在图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.(注意:只需添加一个符合要求的正方形,并用阴影表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地图书馆为了满足群众多样化阅读的需求,决定购买甲、乙两种品牌的电脑若干组建电子阅览室.经了解,甲、乙两种品牌的电脑单价分别3100元和4600元.
(1)若购买甲、乙两种品牌的电脑共50台,恰好支出200000元,求甲、乙两种品牌的电脑各购买了多少台?
(2)若购买甲、乙两种品牌的电脑共50台,每种品牌至少购买一台,且支出不超过160000元,共有几种购买方案?并说明哪种方案最省钱.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com