
【题目】为弘扬中华传统文化,我市某中学决定根据学生的兴趣爱好组建课外兴趣小组,因此学校随机抽取了部分同学的兴趣爱好进行调查,将收集的数据整理并绘制成下列两幅统计图,请根据图中的信息,完成下列问题:
(1)学校这次调查共抽取了 名学生;
(2)补全条形统计图;
(3)在扇形统计图中,“戏曲”所在扇形的圆心角度数为 ;
(4)设该校共有学生2000名,请你估计该校有多少名学生喜欢书法?
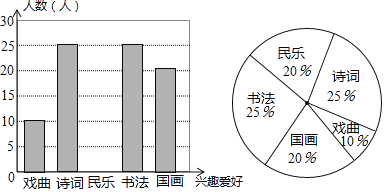
【答案】(1)100;(2)补全图形见解析;(3)36°;(4)估计该校喜欢书法的学生人数为500人.
【解析】(1)用“戏曲”的人数除以其所占百分比可得;
(2)用总人数乘以“民乐”人数所占百分比求得其人数,据此即可补全图形;
(3)用360°乘以“戏曲”人数所占百分比即可得;
(4)用总人数乘以样本中“书法”人数所占百分比可得.
(1)学校本次调查的学生人数为10÷10%=100名,
故答案为:100;
(2)“民乐”的人数为100×20%=20人,
补全图形如下:
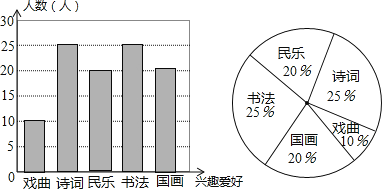
(3)在扇形统计图中,“戏曲”所在扇形的圆心角度数为360°×10%=36°,
故答案为:36°;
(4)估计该校喜欢书法的学生人数为2000×25%=500人.


 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源: 题型:
【题目】随着柴静纪录片《穹顶之下》的播出,全社会对空气污染问题越来越重视,空气净化器的销量也大增,商社电器从厂家购进了A,B两种型号的空气净化器,已知一台A型空气净化器的进价比一台B型空气净化器的进价多300元,用7500元购进A型空气净化器和用6000元购进B型空气净化器的台数相同.
(1)求一台A型空气净化器和一台B型空气净化器的进价各为多少元?
(2)在销售过程中,A型空气净化器因为净化能力强,噪音小而更受消费者的欢迎.为了增大B型空气净化器的销量,商社电器决定对B型空气净化器进行降价销售,经市场调查,当B型空气净化器的售价为1800元时,每天可卖出4台,在此基础上,售价每降低50元,每天将多售出1台,如果每天商社电器销售B型空气净化器的利润为3200元,请问商社电器应将B型空气净化器的售价定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知抛物线y=x2-bx+5与x轴交于A,B两点,与y轴交于点C,已知点A的坐标是(1,0),点A在点B的左边.
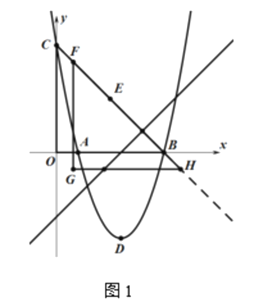
(1)求抛物线的函数解析式;
(2)如图1,点E为BC的中点,将△BOC沿CE方向进行平移,平移后得到的三角形为△HGF,当点F与点E重合时停止运动.设平移的距离CF=m,记△HGF在直线l:y=x-3下方的图形面积为S,求S关于m的函数解析式;
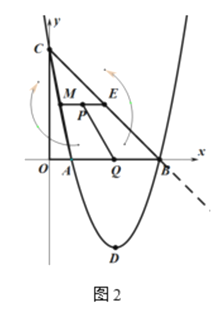
(3)如图2,连结AC和BC,点M,E分别是AC, BC的中点.点P是线段ME上任一点,点Q是线段AB上任一点.现进行如下两步操作:
第一步:沿三角形CAB的中位线ME将纸片剪成两部分,并在线段ME上任意取一点P,线段AB上任意取一点Q,沿PQ将四边形纸片MABE剪成两部分;
第二步:将PQ左侧纸片绕M点按顺时针方向旋转180°,使线段MA与MC重合,将PQ右侧纸片绕E点按逆时针方向旋转180°,使线段EC与EB重合,拼成一个与三角形纸片ABC面积相等的四边形纸片.(注:裁剪和拼图过程均无缝且不重叠)
求拼成的这个四边形纸片的周长的最小值与最大值的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为3的正方形纸片ABCD对折,使AB与DC重合,折痕为EF,展平后,再将点B折到边CD上,使边AB经过点E,折痕为GH,点B的对应点为M,点A的对应点为N,那么折痕GH的长为_____.
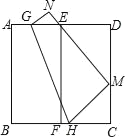
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=a(x﹣1)2+k(a>0)经过点(﹣1,0),顶点为M,过点P(0,a+4)作x轴的平行线1,l与抛物线及其对称轴分别交于点A,B,H.以下结论:①当x=3.1时,y>0;②存在点P,使AP=PH;③(BP﹣AP)是定值;④设点M关于x轴的对称点为M',当a=2时,点M′在l下方,其中正确的是( )

A. ①③B. ②③C. ②④D. ①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,弹性小球从点P(0,3)出发,沿所示方向运动,每当小球碰到矩形OABC的边时反弹,反弹时反射角等于入射角,当小球第1次碰到矩形的边时的点为P1,第2次碰到矩形的边时的点为P2,…,第n次碰到矩形的边时的点为Pn,则点P2的坐标是_____,点P2017的坐标是_____.
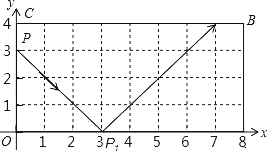
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是边长为10的菱形,对角线AC、BD相交于点E,过点C作CF∥DB交AB延长线于点F,联结EF交BC于点H.
(1)如图1,当EF⊥BC时,求AE的长;
(2)如图2,以EF为直径作⊙O,⊙O经过点C交边CD于点G(点C、G不重合),设AE的长为x,EH的长为y;
①求y关于x的函数关系式,并写出定义域;
②联结EG,当△DEG是以DG为腰的等腰三角形时,求AE的长.
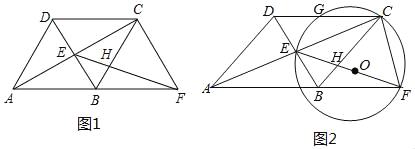
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知E、F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M,则下列结论:①∠AME=90°;②∠BAF=∠EDB;③MD=2AM=4EM;④AM=![]() MF.其中正确结论的个数是( )
MF.其中正确结论的个数是( )
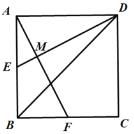
A. 4个B. 3个C. 2个D. 1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com