
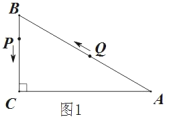
【题目】已知,如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .动点
.动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 向点
向点![]() 运动,动点
运动,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 向点
向点![]() 运动,如果动点
运动,如果动点![]() 以1
以1![]() ,
,![]() 以2
以2![]() 的速度同时出发,设运动时间为
的速度同时出发,设运动时间为![]() ,解答下列问题:
,解答下列问题:
(1)当![]() __________
__________![]() 时,
时,![]() ;
;
(2)连接![]() .
.
①当![]() 时,求线段
时,求线段![]() 的长;
的长;
②在运动过程中,![]() 的形状不断发生变化,它能否构成直角三角形?如果能则求出此时
的形状不断发生变化,它能否构成直角三角形?如果能则求出此时![]() 的值,如果不能,请说明理由.
的值,如果不能,请说明理由.
【答案】(1)6;(2)①![]() ,②能,当t为4.5或7.2时,△BPQ是直角三角形.
,②能,当t为4.5或7.2时,△BPQ是直角三角形.
【解析】
(1)先求得AB的长,再设BP=t,AQ=2t,则BQ=18-2t,即可求得t的值;
(2)①作QM⊥BC于M,QN⊥AC于N,在Rt△PQM中,利用勾股定理即可求解;
②分两种情况讨论当PQ⊥BC和PQ⊥BA,利用直角三角形的性质解答即可.
(1)在Rt△ABC中,∠C=90°,∠A=30°,BC=9 cm
∴AB=2 BC =18 cm,
由P、Q的运动速度可知:BP=t,AQ=2t,则BQ=18-2t,
根据题意:BP=BQ,即t=18-2t,
解得:t=6(s);
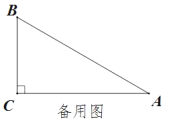
(2)在Rt△ABC中,∠C=90°,∠A=30°,BC=9 cm.
∴AB=18 cm,AC=![]() =
=![]() cm,
cm,
由P、Q的运动速度可知:BP=t,AQ=2t,
①当t=4时, BP=4,AQ=8,

作QM⊥BC于M,QN⊥AC于N,如答图1,
∵![]() ,
,
∴四边形CNQM为矩形,MC= QN,QM=CN,
∵∠A=30°,AQ=8,
∴QN=![]() ,
,![]() ,
,
∴PM=BC-BP-MC=9﹣4﹣4=1,
QM=CN=AC﹣AN=![]() ,
,
∴![]() (cm);
(cm);
②能构成直角三角形,有以下两种情况:
如答图2,当PQ⊥BC时,即PQ//AC,

∴∠BQP=∠A=30°,
∴BQ=2BP=2t,
即AB=BQ+AQ=2t +2t =4t=18,
解得:t=4.5(s);
如答图3,当PQ⊥BA时,
∵∠A=30°,
∴∠B=60°,
∴∠BPQ=30°,
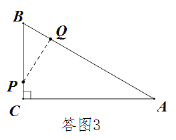
∴BP=2BQ=t,
∴BQ=0.5t,
即AB=AQ+BQ=2t+0.5t =2.5t=18,
解得:t=7.2(s);
综上所述,当t为4.5(s)或7.2(s)时,△BPQ是直角三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(1)计算:![]() ;
;
(2)已知x=![]() +3, y=
+3, y=![]() -3,求下列各式的值:①x2-2xy+y2;②x2-y2;
-3,求下列各式的值:①x2-2xy+y2;②x2-y2;
(3)已知a、b、c满足![]()
求:①a、b、c的值;
②请判断以a、b、c为边构成三角形的形状(按角分类),并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在清江河污水网管改造建设中,需要确保在汛期来临前将建设过程中产生的渣土清运完毕,每天至少需要清运渣土12720m3,施工方准备每天租用大、小两种运输车共80辆.已知每辆大车每天运送渣土200m3,每辆小车每天运送渣土120m3,大、小车每天每辆租车费用分别为1200元,900元,且要求每天租车的总费用不超过85300元.
(1)施工方共有多少种租车方案?
(2)哪种租车方案费用最低,最低费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
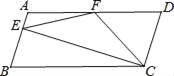
【题目】如图,在ABCD中,AD=2AB,F是AD的中点,E是AB上一点,连接CF、EF、EC,且CF=EF,下列结论正确的个数是( )
①CF平分∠BCD;②∠EFC=2∠CFD;③∠ECD=90°;④CE⊥AB.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,O是等边△ABC内一点,连接OA、OB、OC,且OA=3,OB=4,OC=5,将△BAO绕点B顺时针旋转后得到△BCD,连接OD.求:

①旋转角的度数;
②线段OD的长;
③∠BDC的度数.
(2)如图2所示,O是等腰直角△ABC(∠ABC=90°)内一点,连接OA、OB、OC,将△BAO绕点B顺时针旋转后得到△BCD,连接OD.当OA、OB、OC满足什么条件时,∠ODC=90°?请给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于G,BG=
ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于G,BG=![]() ,则梯形AECD的周长为( )
,则梯形AECD的周长为( )
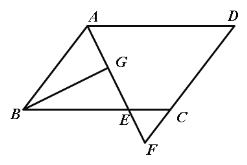
A.22 B.23 C.24 D.25
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 ABCD 中,AE、BF 分别平分∠DAB 和∠ABC,交 CD 于点 E、F,AE、BF 相交于点 M.
(1)求证:AE⊥BF;
(2)判断线段 DF 与 CE 的大小关系,并予以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在5×5的正方形网格中,从在格点上的点A,B,C,D中任取三点,所构成的三角形恰好是直角三角形的个数为( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC 中,AB=AC=BC,∠BDC=120°且BD=DC,现以D为顶点作一个60°角,使角两边分别交AB,AC边所在直线于M,N两点,连接MN,探究线段BM、MN、NC之间的关系,并加以证明.
(1)如图1,若∠MDN的两边分别交AB,AC边于M,N两点.猜想:BM+NC=MN.延长AC到点E,使CE=BM,连接DE,再证明两次三角形全等可证.请你按照该思路写出完整的证明过程;
(2)如图2,若点M、N分别是AB、CA的延长线上的一点,其它条件不变,再探究线段BM,MN,NC之间的关系,请直接写出你的猜想(不用证明).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com