
【题目】如图,在四边形ABCD中,AC平分∠BAD,AD=AC,在AC上截取AE=AB,连接DE、BE,并延长BE交CD于点 F,以下结论:①△BAC≌△EAD;②∠ABE+∠ADE=∠BCD;③BC+CF=DE+EF;其中正确的有( )个

A. 0 B. 1 C. 2 D. 3
【答案】D
【解析】
通过SAS可证明△BAC≌△EAD,即可判断①;由等腰三角形的性质及三角形内角和定理可得出∠ABE=∠ACF,再由全等三角形对应角相等得出∠ACB=∠ADE,即可判断②;通过证明∠FEC=∠FCD,得到EF=CF,再由全等三角形对应边相等得出BC=ED,即可判断③.
∵AC平分∠BAD,∴∠BAC=∠DAC.
在△BAC和△EAD中,∵AB=AE,∠BAC=∠DAC,AC=AD,∴△BAC≌△EAD,故①正确;
设∠BAC=x,则∠DAC=x.
∵AB=AE,∴∠ABE=∠AEB=![]() .
.
∵AC=AD,∴∠ACD=∠ADC=![]() ,∴∠ABE=∠ACF.
,∴∠ABE=∠ACF.
∵△BAC≌△EAD,∴BC=ED,∠ACB=∠ADE,∴∠ABE+∠ADE=∠ACD+∠ACB=∠BCD,故②正确;
∵∠ABE=∠AEB=∠ACD,∠FEC=∠AEB,∴∠FEC=∠FCD,∴EF=CF.
∵BC=ED,∴BC+CF=DE+EF,故③正确.
故选D.


科目:初中数学 来源: 题型:
【题目】如图,A城气象台测得台风中心在A城正西方向320 km的B处,以每小时40 km的速度向北偏东60°的BF方向移动,距离台风中心200 km的范围内是受台风影响的区域.
(1)A城是否受到这次台风的影响?为什么?
(2)若A城受到这次台风影响,那么A城遭受这次台风影响有多长时间?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在ABCD中,E,F分别是边AD,BC上的点,且AE=CF,直线EF分别交BA的延长线、DC的延长线于点G,H,交BD于点O.
(1)求证:△ABE≌△CDF;
(2)连接DG,若DG=BG,则四边形BEDF是什么特殊四边形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)﹣![]() ﹣(+13)+(﹣
﹣(+13)+(﹣![]() )﹣(﹣17)
)﹣(﹣17)
(2)﹣22+3÷(﹣1)2017﹣|﹣4|×5
(3)先化简再求值﹣3(2x2﹣xy)+4(x2+xy﹣6),其中x=﹣1,y=2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于 ![]() 的一元二次方程 x2+(2m-1)x+m2=0有两个实数根 x1 和 x2 .
的一元二次方程 x2+(2m-1)x+m2=0有两个实数根 x1 和 x2 .
(1)求实数 m 的取值范围;
(2)当 x12-x22 时,求 m 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAC=90°,AD⊥BC,垂足为点 D.下列说法中:①∠B的余角只有∠BAD;②∠B=∠C;③线段 AB 的长度表示点 B 到直线 AC 的距离;④AB·AC=BC·AD;一定正确的有( )
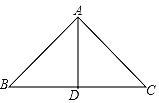
A. 1 个 B. 2 个 C. 3 个 D. 4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2012年6月1日起,国家实施了中央财政补贴条例支持高效节能电器的推广使用,某款定速空调在条例实施后,每购买一台,客户可获财政补贴200元,若同样用11万元所购买的此款空调数台,条例实施后比实施前多10%.求条例实施前此款空调的单价.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com