
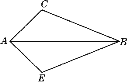
【题目】如图,对角线AB把四边形ACBE分为△ABC和△ABE两部分,如果△ABC中BC边上的高和△ABE中BE边上的高相等,且AC=AE.
(1)在原图上画出△ABC中BC边上的高AD与△ABE中BE边上的高AF;
(2)请你猜想BC与BE的数量关系并证明.
【答案】(1)见解析;(2)BC=BE.
【解析】
(1)根据作三角形的高的方法,作出AD、AF;
(2)根据HL证明Rt△ACD≌Rt△AEF,从而得出CD=EF,再根据HL证明Rt△ABD≌Rt△ABF,从而得出BD=BF,再利用等式的性质得出:BD-CD=BF-EF,即BC=BE.
解:(1)画出高AD,AF,如图所示.
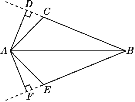
(2)猜想:BC=BE.证明如下:
∵AD⊥BC,AF⊥BE,
∴△ACD,△AEF,△ABD,△ABF都是直角三角形.
在Rt△ACD和Rt△AEF中,
![]()
∴Rt△ACD≌Rt△AEF(HL).
∴CD=EF(全等三角形的对应边相等).
在Rt△ABD和Rt△ABF中,
![]()
∴Rt△ABD≌Rt△ABF(HL).
∴BD=BF(全等三角形的对应边相等).
∴BD-CD=BF-EF(等式的性质),即BC=BE.


科目:初中数学 来源: 题型:
【题目】将下列各数填入相应的大括号内:
3.141 592 6,![]() ,
,![]() ,-6,8,
,-6,8,![]() ,2-π,0.014 545 454 5…,-
,2-π,0.014 545 454 5…,-![]() ,0,
,0,![]() ,0.323 223 222 3….
,0.323 223 222 3….
(1)有理数:{ …};
(2)无理数:{ …};
(3)正无理数:{ …};
(4)整数:{ …}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AD⊥BC于点D,E为AB边上任意一点,EF⊥BC于点F,∠1=∠2.求证:DG∥AB.请把证明的过程填写完整.
证明:∵AD⊥BC,EF⊥BC( ),
∴∠EFB=∠ADB=90°(垂直的定义)
∴EF∥ ( )
∴∠1= ( )
又∵∠1=∠2(已知)
∴ ( )
∴DG∥AB( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知点E,F,G,H是矩形ABCD各边的中点,AB=6,BC=8,动点M从点E出发,沿E→F→G→H→E匀速运动,设点M运动的路程x,点M到矩形的某一个顶点的距离为y,如果表示y关于x函数关系的图象如图2所示,那么这个顶点是矩形的( )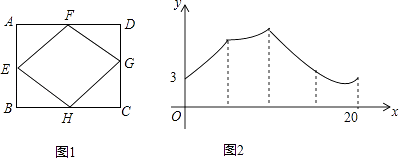
A.点A
B.点B
C.点C
D.点D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 不能确定
D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点P(x,y),如果点Q(x,y′)的纵坐标满足y′= ![]() ,那么称点Q为点P的“关联点”.
,那么称点Q为点P的“关联点”.
(1)请直接写出点(3,5)的“关联点”的坐标;
(2)如果点P在函数y=x﹣2的图象上,其“关联点”Q与点P重合,求点P的坐标;
(3)如果点M(m,n)的“关联点”N在函数y=2x2的图象上,当0≤m≤2时,求线段MN的最大值.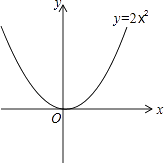
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4) 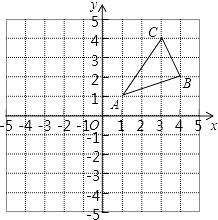 .
.
(1)请画出△ABC关于原点对称的△A2B2C2;并写出各点的坐标.
(2)在x轴上求作一点P,使△PAB的周小最小,请画出△PAB,并直接写出P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠C=90°,AC=BC=4cm,D是AB的中点,以C为圆心,4cm长为半径作圆,则A,B,C,D四点中,在圆内的有( )
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某施工工地安放了一个圆柱形饮水桶的木制支架(如图1),若不计木条的厚度,其俯视图如图2所示,已知AD垂直平分BC,AD=BC=48cm,则圆柱形饮水桶的底面半径的最大值是cm. 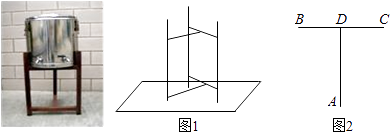
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com