
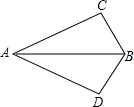
 如图,在△ABC和△ABD中,∠C=∠D=90°,若利用“HL”证明△ABC≌△ABD,则需要加条件BC=BD或AC=AD.
如图,在△ABC和△ABD中,∠C=∠D=90°,若利用“HL”证明△ABC≌△ABD,则需要加条件BC=BD或AC=AD. 分析 本题要判定△ABC≌△ABD,已知∠C=∠D=90°,AB=AB,具备了一组边、一组角相等,故添加∠CAB=∠DAB或∠CBA=∠DBA,BD=BC或AD=AC后可分别根据AAS、HL判定三角形全等.
解答 解:添加∠CAB=∠DAB或∠CBA=∠DBA,BD=BC或AD=AC.
∵∠C=∠D,∠CAB=∠DAB(∠CBA=∠DBA),AB=AB
∴△ABC≌△ABD(AAS);
∵∠C=∠D=90°,AB=AB(AD=AC),BD=BC
∴△ABC≌△ABD(HL).
故答案为BC=BD或AC=AD.
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.


科目:初中数学 来源: 题型:解答题
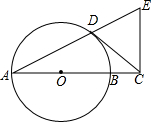 已知AB为⊙O的直径,点D为⊙O上一点,过点D作⊙O的切线,交AB的延长线于点C,过点C作AC的垂线,交AD的延长线于点E
已知AB为⊙O的直径,点D为⊙O上一点,过点D作⊙O的切线,交AB的延长线于点C,过点C作AC的垂线,交AD的延长线于点E查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=$\sqrt{5}$ b=2 c=3 | B. | a=7 b=24 c=5 | C. | a=6 b=8 c=10 | D. | a=3 b=4 c=5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 摸出一个红球的可能性大 | B. | 摸出一个白球的可能性大 | ||
| C. | 两种可能性一样大 | D. | 无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com